第10章 在策略控制近似方法

在本章中，我们回到控制问题，现在使用动作-价值函数 \(\hat{q}(s,a,\mathbf{w})\approx q_{*}(s, a)\) 的参数近似， 其中 \(\mathbf{w} \in \mathbb{R}^{d}\) 是有限维权重向量。我们继续只关注在策略情况，将离策略方法留给第11章。 本章以半梯度Sarsa算法为特征，将半梯度TD(0)（最后一章）自然延伸到动作价值和策略控制。 在回合案例中，扩展是直截了当的，但在持续的情况下，我们必须向后退几步并重新审视我们如何使用折扣来定义最优策略。 令人惊讶的是，一旦我们有真正的函数近似，我们就必须放弃折扣并转而使用新的“差异”价值函数来控制问题的新“平均回报”表达式。

首先从回合案例开始，我们将上一章中提出的函数近似思想从状态值扩展到动作价值。 然后我们扩展它们以控制遵循策略GPI的一般模式，使用 \(\varepsilon\) 贪婪进行动作选择。 我们在陡坡汽车问题上显示n步线性Sarsa的结果。然后我们转向持续的情况并对于具有不同价值的平均奖励案例重复开发这些想法。

10.1 回合半梯度控制

将第9章的半梯度预测方法扩展到动作价值是很简单的。在这种情况下，它是近似动作价值函数 \(\hat{q} \approx q_{\pi}\)， 其表示为具有权重向量 \(\mathbf{w}\) 的参数化函数形式。 而在我们考虑 \(S_{t} \mapsto U_{t}\) 形式的随机训练示例之前， 现在我们考虑 \(S_{t}, A_{t} \mapsto U_{t}\) 形式的例子。 更新目标 \(U_{t}\) 可以是 \(q_{\pi}\left(S_{t}, A_{t}\right)\) 的任何近似值，包括通常的备份值， 例如完整的蒙特卡罗回报（\(G_{t}\)）或任何n步Sarsa回报（7.4）。动作价值预测的一般梯度下降更新是

(1)\[\mathbf{w}_{t+1} \doteq \mathbf{w}_{t}+\alpha\left[U_{t}-\hat{q}\left(S_{t}, A_{t}, \mathbf{w}_{t}\right)\right] \nabla \hat{q}\left(S_{t}, A_{t}, \mathbf{w}_{t}\right)\]

例如，一步Sarsa方法的更新是

(2)\[\mathbf{w}_{t+1} \doteq \mathbf{w}_{t}+\alpha\left[R_{t+1}+\gamma \hat{q}\left(S_{t+1}, A_{t+1}, \mathbf{w}_{t}\right)-\hat{q}\left(S_{t}, A_{t}, \mathbf{w}_{t}\right)\right] \nabla \hat{q}\left(S_{t}, A_{t}, \mathbf{w}_{t}\right)\]

我们将这种方法称为 回合半梯度一步Sarsa。对于常量策略，此方法以与TD(0)相同的方式收敛， 具有相同类型的误差边界（9.14）。

为了形成控制方法，我们需要将这些动作价值预测方法与策略改进和行动选择技术相结合。 适用于连续动作或来自大型离散集的动作的适当技术是正在进行的研究主题，但尚未明确解决。 另一方面，如果动作集是离散的并且不是太大，那么我们可以使用前面章节中已经开发的技术。 也就是说，对于当前状态 \(S_t\) 中可用的每个可能动作， 我们可以计算 \(\hat{q}\left(S_{t}, a, \mathbf{w}_{t}\right)\)， 然后找到贪婪动作 \(A_t^*=\arg\max _{a} \hat{q}(S_t,a,\mathbf{w}_{t-1})\)。 然后通过将估计策略更改为贪婪策略（例如 \(\varepsilon\) -贪婪策略）的软近似来完成策略改进 （在本章中处理的在策略案例中）。根据相同的策略选择动作。完整算法的伪代码于下框中给出。

回合半梯度Sarsa估计 \(\hat{q} \approx q_*\)

输入：可微分的动作价值函数参数化 \(\hat{q} : \mathcal{S} \times \mathcal{A} \times \mathbb{R}^{d} \rightarrow \mathbb{R}\)

算法参数：步长 \(\alpha>0\)，小 \(\varepsilon>0\)

任意初始化价值函数权重 \(\mathbf{w} \in \mathbb{R}^{d}\) （比如 \(\mathbf{w}=\mathbf{0}\)）

对每个回合循环：

\(S, A \leftarrow\) 初始回合状态和动作（比如 \(\varepsilon\) -贪婪）

对回合每一步循环：

采取动作 \(A\)，观察 \(R, S^{\prime}\)

如果 \(S^{\prime}\) 不是终点：

\(\mathbf{w} \leftarrow \mathbf{w}+\alpha[R-\hat{q}(S, A, \mathbf{w})] \nabla \hat{q}(S, A, \mathbf{w})\)

进入下一个回合

选择 \(A^{\prime}\) 作为 \(\hat{q}\left(S^{\prime}, \cdot, \mathbf{w}\right)\) 的函数（比如 \(\varepsilon\) -贪婪）

\(\mathbf{w} \leftarrow \mathbf{w}+\alpha\left[R+\gamma \hat{q}\left(S^{\prime}, A^{\prime}, \mathbf{w}\right)-\hat{q}(S, A, \mathbf{w})\right] \nabla \hat{q}(S, A, \mathbf{w})\)

\(S \leftarrow S^{\prime}\)

\(A \leftarrow A^{\prime}\)

例10.1：陡坡汽车任务 考虑如图10.1左上图所示，在陡峭的山路上驾驶动力不足的汽车的任务。 困难在于重力比汽车的发动机强，即使在全油门时，汽车也无法陡坡加速。 唯一的解决方案是首先远离目标并向左边相反的斜坡上移动。 然后，通过应用全油门，汽车可以建立足够的惯性，以便将其带到陡坡上，即使它在整个过程中减速。 这是一个连续控制任务的简单示例，在某种意义上，事物必须变得更糟（离目标更远）才能变得更好。 除非得到人类设计师的明确帮助，否则许多控制方法对于此类任务都有很大的困难。

图10.1： 陡坡汽车任务（左上图）和一次运行中学习的成本函数 \(-\max _{a} \hat{q}(s, a, \mathbf{w})\)。

这个问题的奖励在所有时步都是 \(-1\)，直到汽车越过山顶的目标位置，结束了这一回合。 有三种可能的动作：全油门前进（\(+1\)），全油门倒车（\(-1\)）和零油门（\(0\)）。 汽车根据简化的物理学运动。 它的位置 \(x_t\) 和速度 \(\dot{x}_{t}\)，由更新

\[\begin{split}\begin{array}{l} {x_{t+1} \doteq \text{bound}\left[x_{t}+\dot{x}_{t+1}\right]} \\ {\dot{x}_{t+1} \doteq \text{bound}\left[\dot{x}_{t}+0.001 A_{t}-0.0025 \cos \left(3 x_{t}\right)\right]} \end{array}\end{split}\]

其中 \(\text{bound}\) 操作强制 \(-1.2 \leq x_{t+1} \leq 0.5\) 和 \(-0.07 \leq \dot{x}_{t+1} \leq 0.07\)。 另外，当 \(\dot{x}_{t+1}\) 到达左边界时，\(\dot{x}_{t+1}\) 被重置为零。 当它到达右边界时，达到了目标并且回合终止了。每回合从随机位置 \(x_{t} \in[-0.6,-0.4)\) 和零速度开始。 为了将两个连续状态变量转换为二进制特征，我们使用了网格平铺，如图9.9所示。 我们使用8个铺片，每个铺片覆盖每个维度中有界距离的1/8，并且如第9.5.4节所述的非对称偏移 [1]。 然后通过铺片编码创建的特征向量 \(\mathbf{x}(s, a)\) 与线性组合，用于近似动作价值函数的参数向量：

(3)\[\hat{q}(s, a, \mathbf{w}) \doteq \mathbf{w}^{\top} \mathbf{x}(s, a)=\sum_{i=1}^{d} w_{i} \cdot x_{i}(s, a)\]

对于每对状态 \(s\) 和动作 \(a\)。

图10.1显示了在学习使用这种形式的函数近似来解决此任务时通常会发生的情况 [2]。 显示的是在单次运行中学习的价值函数（成本（cost- to-go） 函数）的负数。 初始动作值均为零，这是乐观的（在此任务中所有真值均为负值），即使探测参数 \(\varepsilon\) 为0，也会导致进行大量探索。 这可以在中间的顶部面板中看到，图中标有“Step 428”。此时甚至没有一个回合完成，但是汽车在山谷中来回摆动，沿着状态空间的圆形轨迹。 所有经常访问的状态都比未开发状态更糟糕，因为实际的奖励比（不切实际的）预期更糟糕。 这会不断推动个体远离任何地方，探索新的状态，直到找到解决方案。

图10.2显示了此问题的半梯度Sarsa的几条学习曲线，具有不同的步长。

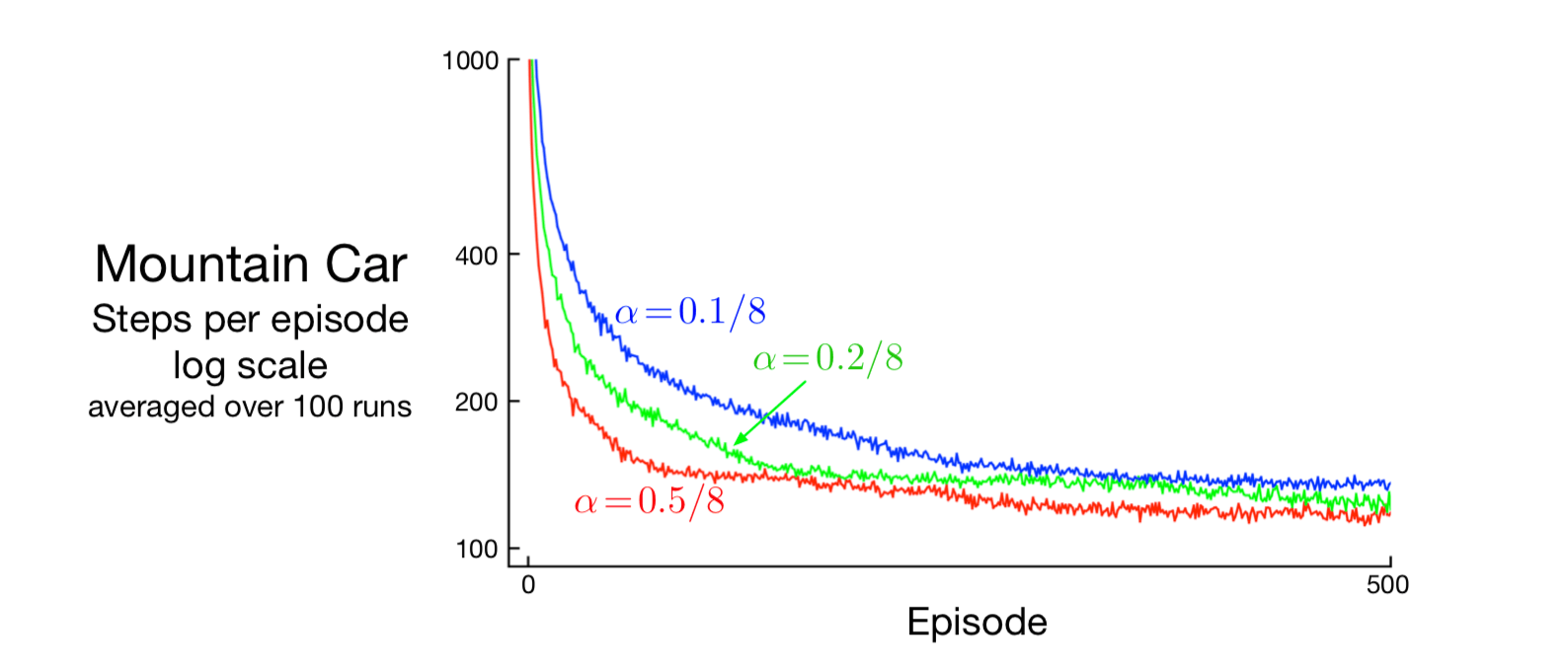
图10.2： 具有铺片编码函数近似和 \(\varepsilon\) -贪婪动作选择的半梯度Sarsa方法的陡坡汽车任务学习曲线。

10.2 半梯度n步Sarsa

我们可以通过在半梯度Sarsa更新方程（10.1）中使用n步回报作为更新目标来获得回合半梯度Sarsa的n步版本。 n步回报立即从其表格形式（7.4）推广到函数近似形式：

(4)\[G_{t : t+n} \doteq R_{t+1}+\gamma R_{t+2}+\cdots+\gamma^{n-1} R_{t+n}+\gamma^{n} \hat{q}\left(S_{t+n}, A_{t+n}, \mathbf{w}_{t+n-1}\right), \quad t+n<T\]

其中 \(G_{t:t+n}=G_{t}\) 如果 \(t+n \geq T\)，像往常一样。 n步更新方程是

(5)\[\mathbf{w}_{t+n} \doteq \mathbf{w}_{t+n-1}+\alpha\left[G_{t : t+n}-\hat{q}\left(S_{t}, A_{t}, \mathbf{w}_{t+n-1}\right)\right] \nabla \hat{q}\left(S_{t}, A_{t}, \mathbf{w}_{t+n-1}\right), \quad 0 \leq t<T\]

完整的伪代码在下面的框中给出：

回合半梯度n步Sarsa估计 \(\hat{q} \approx q_*\) 或 \(q_\pi\)

输入：可微分的动作价值函数参数化 \(\hat{q} : \mathcal{S} \times \mathcal{A} \times \mathbb{R}^{d} \rightarrow \mathbb{R}\)

输入：一个策略 \(\pi\) （如果估计 \(q_\pi\)）

算法参数：步长 \(\alpha>0\)，小 \(\varepsilon>0\)，一个正整数 \(n\)

任意初始化价值函数权重 \(\mathbf{w} \in \mathbb{R}^{d}\) （比如 \(\mathbf{w}=\mathbf{0}\)）

所有存储和访问操作（\(S_t\)，\(A_t\) 和 \(R_t\)）都可以使用它们的索引 \(mod n+1\)

对每个回合循环：

初始化并存储 \(S_0 \ne\) 终点

选择并存储动作 \(A_0 \sim \pi(\cdot | S_0)\) 或者关于 \(\hat{q}(S_{0}, \cdot, \mathbf{w})\) \(\varepsilon\) -贪婪

\(S, A \leftarrow\) 初始回合状态和动作（比如 \(\varepsilon\) -贪婪）

\(T \leftarrow \infty\)

对 \(t=0,1,2,cdots\) 循环：

如果 \(t<T\)，则：

采取动作 \(A_t\)

观察和存储下一个奖励为 \(R_{t+1}\) 和下一个状态为 \(S_{t+1}\)

如果 \(S_{t+1}\) 是终点，则：

\(T=t+1\)

否则：

选择并存储动作 \(A_{t+1} \sim \pi(\cdot | S_{t+1})\) 或者关于 \(\hat{q}(S_{t+1}, \cdot, \mathbf{w})\) \(\varepsilon\) -贪婪

\(\tau \leftarrow t-n+1\) （\(\tau\) 是其估算值正在更新的时间）

如果 \(\tau \geq 0\)：

\(G \leftarrow \sum_{i=\tau+1}^{\min (\tau+n, T)} \gamma^{i-\tau-1} R_{i}\)

如果 \(\tau+n<T\) 则 \(G\leftarrow G+\gamma^n \hat{q}\left(S_{\tau+n}, A_{\tau+n}, \mathbf{w}\right) \quad\) （\(G_{\tau:\tau+n}\)）

\(\mathbf{w} \doteq \mathbf{w}+\alpha\left[G-\hat{q}\left(S_{t}, A_{t}, \mathbf{w}\right)\right] \nabla \hat{q}\left(S_{\tau}, A_{\tau}, \mathbf{w}\right)\)

直到 \(\tau=T-1\)

正如我们之前看到的，如果使用中等级别的自举，性能最佳，对应于大于1的n。 图10.3显示了该算法陡坡汽车任务中在 \(n=8\) 时比在 \(n=\infty\) 处更快地学习并获得更好的渐近性能。 图10.4显示了参数 \(\alpha\) 和 \(n\) 对该任务学习率的影响的更详细研究结果。

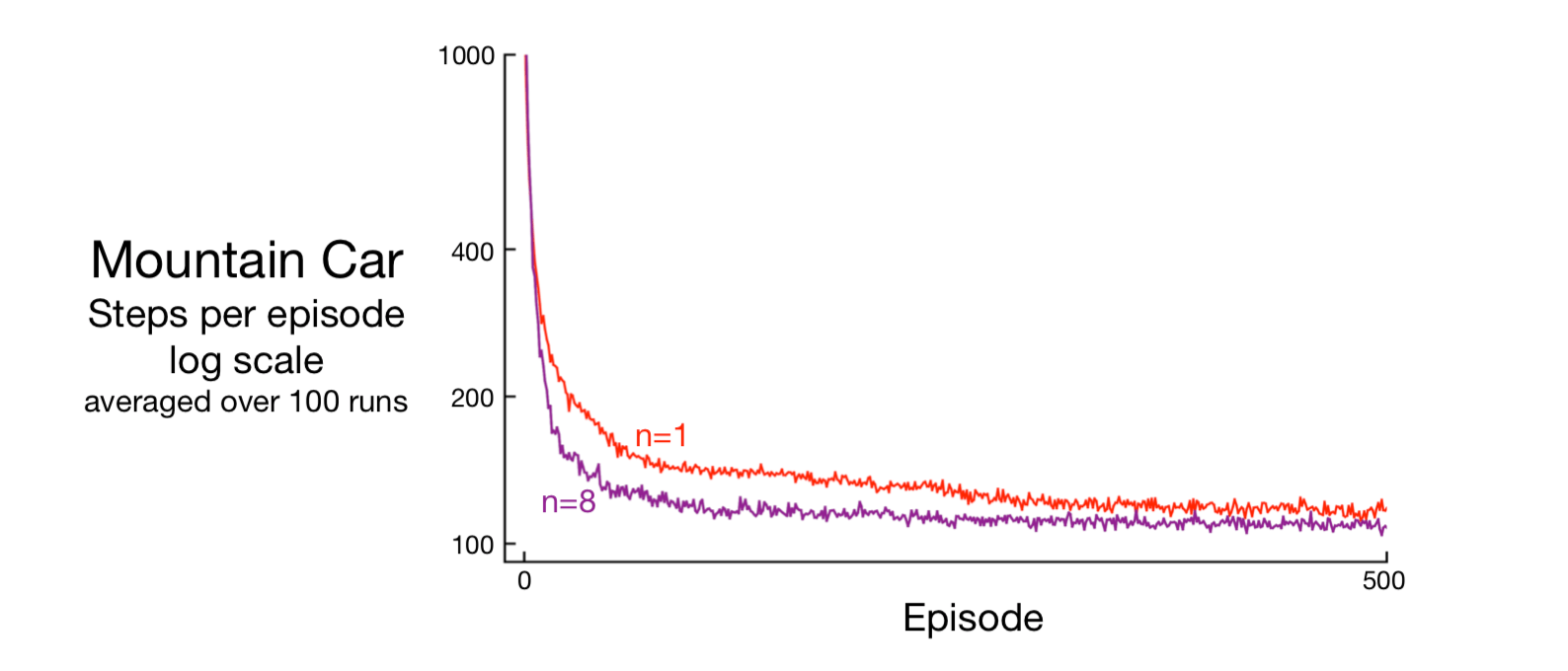
图10.3： 陡坡汽车任务中一步与八步半梯度Sarsa的表现。使用了良好的步长： \(n=1\) 时 \(\alpha=0.5/8\) 且 \(n=8\) 时 \(\alpha=0.3/8\)。

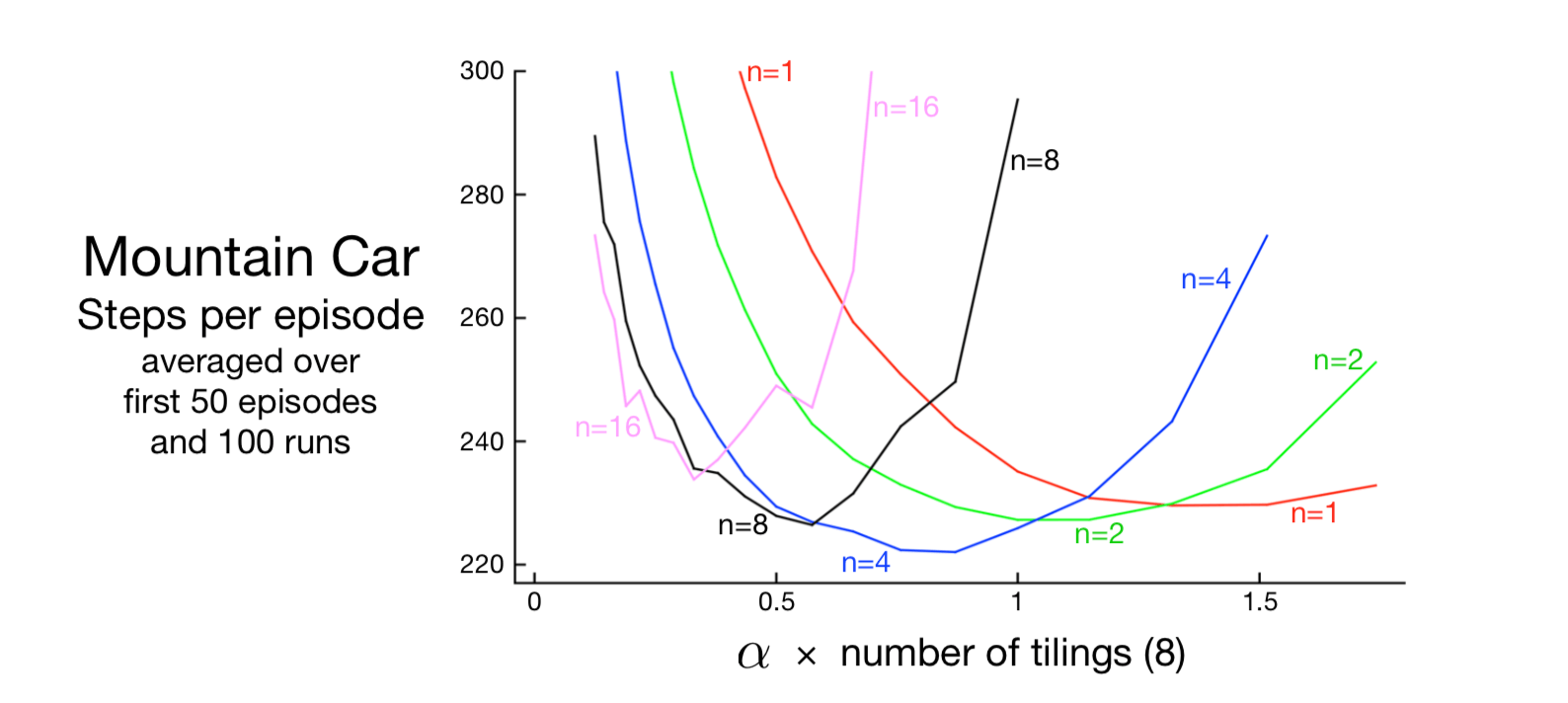
图10.4： \(\alpha\) 和 \(n\) 对陡坡汽车任务的n步半梯度Sarsa和铺片编码函数近似的早期性能的影响。 像往常一样，中等的自举（\(n=4\)）表现最佳。这些结果用于选定的 \(\alpha\) 值，以对数刻度，然后通过直线连接。 对于 \(n=16\)，标准误差范围从 \(n=1\) 时0.5（小于线宽）到大约 \(n=16\) 时4，因此主要影响都是统计上显着的。

练习10.1 在本章中，我们没有明确考虑或给出任何蒙特卡罗方法的伪代码。他们会是什么样的？ 为什么不为它们提供伪代码是合理的？他们将如何在陡坡汽车任务上表现？

练习10.2 给出关于控制的半梯度一步 预期 Sarsa提供伪代码。

练习10.3 为什么图10.4中显示的结果在大 \(n\) 处比在小 \(n\) 处具有更高的标准误差？

10.3 平均奖励：持续任务的新问题设置

我们现在引入第三个经典设置──与回合和折扣设置一起，用于制定马尔可夫决策问题（MDP）中的目标。 与折扣设置一样，平均奖励 设置适用于持续存在的问题，即个体与环境之间的交互在没有终止或启动状态的情况下持续进行的问题。 然而，与那种情况不同的是，没有折扣──个体对延迟奖励的关注与对即时奖励的关注一样多。 平均奖励设置是经典动态规划理论中常用的主要设置之一，在强化学习中较少见。 正如我们在下一节中讨论的那样，折扣设置在功能近似方面存在问题，因此需要平均奖励设置来替换它。

在平均奖励设置中，策略 \(\pi\) 的质量被定义为平均奖励率，或简称为 平均奖励， 同时遵循该策略，我们将其表示为 \(r(\pi)\)：

\[\begin{split}\begin{aligned} r(\pi) & \doteq \lim _{h \rightarrow \infty} \frac{1}{h} \sum_{t=1}^{h} \mathbb{E}\left[R_{t} | S_{0}, A_{0 : t-1} \sim \pi\right] && \text{(10.6)}\\ &=\lim _{t \rightarrow \infty} \mathbb{E}\left[R_{t} | S_{0}, A_{0 : t-1} \sim \pi\right] && \text{(10.7)}\\ &=\sum_{s} \mu_{\pi}(s) \sum_{a} \pi(a | s) \sum_{s^{\prime}, r} p\left(s^{\prime}, r | s, a\right) r \end{aligned}\end{split}\]

期望取决于初始状态 \(S_0\)，以及按照 \(\pi\) 的 后续动作 \(A_{0}, A_{1}, \dots, A_{t-1}\)，\(\mu_\pi\) 是稳态分布， \(\mu_{\pi}(s) \doteq \lim_{t \rightarrow \infty} Pr\left\{S_{t}=s | A_{0:t-1} \sim \pi\right\}\)， 假设存在于任何 \(\pi\) 并且独立于 \(S_0\)。关于MDP的这种假设被称为 遍历性（ergodicity）。 这意味着MDP启动或个体做出的任何早期决策只会产生暂时影响；从长远来看，处于一个状态的期望仅取决于策略和MDP转移概率。 遍历性足以保证上述等式中存在极限。

在未折现的持续情况中，可以在不同类型的最优性之间进行微妙的区分。 然而，对于大多数实际目的而言，简单地根据每个时间步的平均奖励来订购策略可能就足够了，换句话说，根据他们的 \(r(\pi)\)。 如（10.7）所示，该数量基本上是 \(\pi\) 下的平均回报。 特别是，我们认为所有达到 \(r(\pi)\) 最大值的策略都是最优的。

请注意，稳态分布是特殊分布，在该分布下，如果根据 \(\pi\) 选择动作，则保留在同一分布中。也就是说，为此

(6)\[\sum_{s} \mu_{\pi}(s) \sum_{a} \pi(a | s) p\left(s^{\prime} | s, a\right)=\mu_{\pi}\left(s^{\prime}\right)\]

在平均奖励设置中，回报是根据奖励与平均奖励之间的差来定义的：

(7)\[G_{t} \doteq R_{t+1}-r(\pi)+R_{t+2}-r(\pi)+R_{t+3}-r(\pi)+\cdots\]

这称为 差分 回报，相应的值函数称为 差分 价值函数。 它们以相同的方式定义，我们将一如既往地使用相同的符号： \(v_{\pi}(s) \doteq \mathbb{E}_{\pi}\left[G_{t} | S_{t}=s\right]\) 和 \(q_{\pi}(s, a) \doteq \mathbb{E}_{\pi}\left[G_t|S_{t}=s, A_{t}=a\right]\) （类似于 \(v_*\) 和 \(q_*\)）。 差分价值函数也有Bellman方程，与我们之前看到的略有不同。 我们只是删除所有 \(\gamma s\) 并通过奖励和真实平均奖励之间的差替换所有奖励

\[\begin{split}\begin{array}{l} {v_{\pi}(s)=\sum_{a} \pi(a | s) \sum_{r, s^{\prime}} p\left(s^{\prime}, r | s, a\right)\left[r-r(\pi)+v_{\pi}\left(s^{\prime}\right)\right]} \\ {q_{\pi}(s, a)=\sum_{r, s^{\prime}} p\left(s^{\prime}, r | s, a\right)\left[r-r(\pi)+\sum_{a^{\prime}} \pi\left(a^{\prime} | s^{\prime}\right) q_{\pi}\left(s^{\prime}, a^{\prime}\right)\right]} \\ {v_{*}(s)=\max _{a} \sum_{r, s^{\prime}} p\left(s^{\prime}, r | s, a\right)\left[r-\max _{\pi} r(\pi)+v_{*}\left(s^{\prime}\right)\right], \text { 以及 }} \\ {q_{*}(s, a)=\sum_{r, s^{\prime}} p\left(s^{\prime}, r | s, a\right)\left[r-\max _{\pi} r(\pi)+\max _{a^{\prime}} q_{*}\left(s^{\prime}, a^{\prime}\right)\right]} \end{array}\end{split}\]

（参见（3.14），练习3.17，（3.19）和（3.20））。

还存在两种TD误差的差分形式：

(8)\[\delta_{t} \doteq R_{t+1}-\overline{R}_{t}+\hat{v}\left(S_{t+1}, \mathbf{w}_{t}\right)-\hat{v}\left(S_{t}, \mathbf{w}_{t}\right)\]

以及

(9)\[\delta_{t} \doteq R_{t+1}-\overline{R}_{t}+\hat{q}\left(S_{t+1}, A_{t+1}, \mathbf{w}_{t}\right)-\hat{q}\left(S_{t}, A_{t}, \mathbf{w}_{t}\right)\]

其中 \(\overline{R}_{t}\) 是平均奖励 \(r(\pi)\) 在时间 \(t\) 的估计值。 通过这些替代定义，我们的大多数算法和许多理论结果都可以在不改变的情况下进行平均奖励设置。

例如，半梯度Sarsa的平均奖励版本定义如（10.2），除了TD误差版本的不同。也就是说

(10)\[\mathbf{w}_{t+1} \doteq \mathbf{w}_{t}+\alpha \delta_{t} \nabla \hat{q}\left(S_{t}, A_{t}, \mathbf{w}_{t}\right)\]

由（10.11）给出的 \(t\)。完整算法的伪代码在下框中给出。

差分半梯度Sarsa估计 \(\hat{q} \approx q_*\)

输入：可微分的动作价值函数参数化 \(\hat{q} : \mathcal{S} \times \mathcal{A} \times \mathbb{R}^{d} \rightarrow \mathbb{R}\)

算法参数：步长 \(\alpha,\beta>0\)

任意初始化价值函数权重 \(\mathbf{w} \in \mathbb{R}^{d}\) （比如 \(\mathbf{w}=\mathbf{0}\)）

任意初始化平均奖励估计 \(\overline{R} \in \mathbb{R}\) （比如 \(\overline{R}=0\)）

初始化动作 \(S\)，状态 \(A\)

对每个回合循环：

采取动作 \(A\)，观察 \(R, S^{\prime}\)

选择 \(A^{\prime}\) 作为 \(\hat{q}\left(S^{\prime}, \cdot, \mathbf{w}\right)\) 的函数（比如 \(\varepsilon\) -贪婪）

\(\delta \leftarrow R-\overline{R}+\hat{q}\left(S^{\prime}, A^{\prime}, \mathbf{w}\right)-\hat{q}(S, A, \mathbf{w})\)

\(\overline{R} \leftarrow \overline{R}+\beta \delta\)

\(\overline{R} \leftarrow \overline{R}+\beta \delta\)

\(\mathbf{w} \leftarrow \mathbf{w}+\alpha \delta \nabla \hat{q}(S, A, \mathbf{w})\)

\(S \leftarrow S^{\prime}\)

\(A \leftarrow A^{\prime}\)

练习10.4 为半梯度Q-learning的差分版本提供伪代码。

练习10.5 需要哪些方程式（除了10.10）来指定TD(0)的差分版本？

练习10.6 假设有一个MDP在任何策略下产生确定性的奖励序列 \(+1,0,+1,0,+1,0, \dots\) 一直继续下去。 从技术上讲，这是不允许的，因为它违反了遍历性；没有静态极限分布 \(\mu_\pi\)，并且不存在极限（10.7）。 然而，平均奖励（10.6）是明确的；它是什么？现在考虑这个MDP中的两个状态。 从 A 开始，奖励序列完全如上所述，从 \(+1\) 开始， 而从 B 开始，奖励序列以 \(0\) 开始，然后继续 \(+1,0,+1,0, \ldots\)。 对于这种情况，差分回报（10.9）没有很好地定义，因为不存在限制。为了修复这个问题，可以交替地将状态值定义为

(11)\[v_{\pi}(s) \doteq \lim _{\gamma \rightarrow 1} \lim _{h \rightarrow \infty} \sum_{t=0}^{h} \gamma^{t}\left(\mathbb{E}_{\pi}\left[R_{t+1} | S_{0}=s\right]-r(\pi)\right)\]

根据这个定义，状态 A 和 B 的值是多少？

练习10.7 考虑马尔可夫奖励过程，该过程由三个状态 A，B 和 C 组成， 状态转换确定性地围绕环。到达 A 时会收到 \(+1\) 的奖励，否则奖励为 \(0\)。 使用（10.13）的三个状态的差分值是多少？

练习10.8 本节的方框中的伪代码使用 \(\delta_t\) 作为误差而 不是简单的 \(R_{t+1}-\overline{R}_{t}\) 更新 \(\overline{R}_{t}\)。 这两个误差都有效，但使用 \(\delta_t\) 更好。要了解原因，请考虑练习10.7中三个状态的环形MRP。 平均奖励的估计应倾向于其真实值 \(\frac{1}{3}\)。 假设它已经存在并被卡在那里。 \(R_{t+1}-\overline{R}_{t}\) 误差的序列是什么？ \(\delta_{t}\) 误差的序列是什么（使用（10.10））？ 如果允许估计价值因误差而改变，哪个误差序列会产生更稳定的平均回报估计值？ 为什么？

例10.2：访问控制排队任务 这是一个涉及对一组10台服务器的访问控制的决策任务。 有四个不同优先级的客户到达一个队列。如果允许访问服务器，则客户向服务器支付1,2,4或8的奖励， 具体取决于他们的优先级，优先级较高的客户支付更多。 在每个时步中，队列头部的客户被接受（分配给其中一个服务器）或被拒绝（从队列中移除，奖励为零）。 在任何一种情况下，在下一个时步中，将考虑队列中的下一个客户。队列永远不会清空，队列中客户的优先级随机分布。 当然，如果没有免费服务器，则无法提供服务；在这种情况下，客户总是被拒绝。 每个繁忙的服务器在每个时步都变为空闲，概率 \(p=0.06\)。 虽然我们刚刚将它们描述为明确，但让我们假设到达和离开的统计数据是未知的。 任务是根据优先级和免费服务器的数量来决定是接受还是拒绝下一个客户，以便最大化长期奖励而不折扣。

在这个例子中，我们考虑这个问题的表格解决方案。虽然状态之间没有泛化， 但我们仍然可以在通用函数近似设置中考虑它，因为此设置泛化了表格设置。 因此，我们对每对状态（空闲服务器的数量和队列头部的客户的优先级）和操作（接受或拒绝）进行了不同的动作-价值估计。 图10.5显示了差分半梯度Sarsa求解的解， 参数 \(\alpha=0.01\)，\(\beta=0.01\)，\(\varepsilon=0.1\)。 初始动作价值和 \(\overline{R}\) 为零。

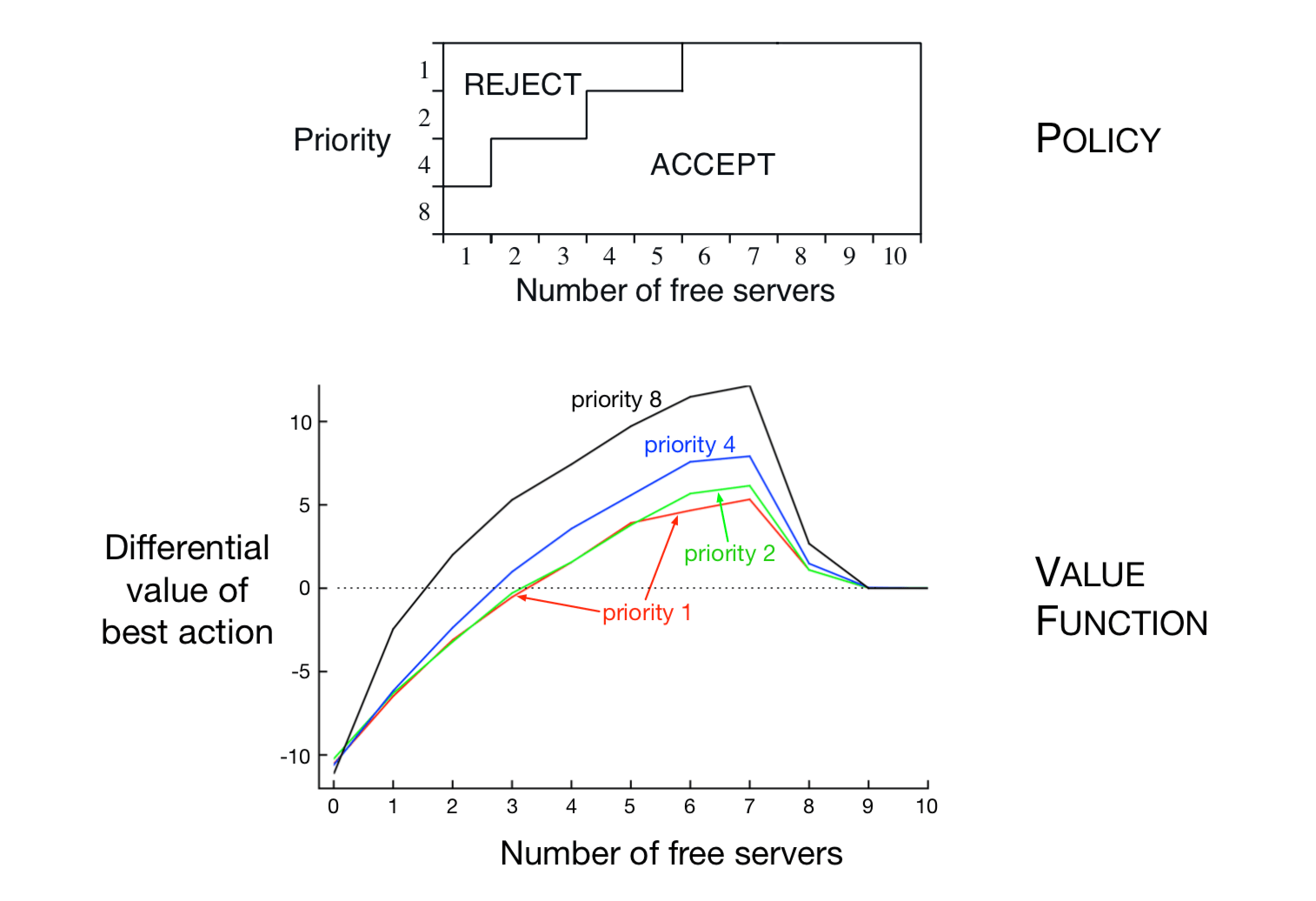
图10.5：差分半梯度一步法Sarsa在200万步后的访问控制排队任务中找到的策略和价值函数。 图表右侧的下降可能是由于数据不完善；许多这些状态从未经历过。\(\overline{R}\) 学习的价值约为2.31。

10.4 弃用折扣设置

在表格案例中，持续的折扣问题表达非常有用，其中每个状态的回报可以单独识别和平均。 但在大致情况下，是否应该使用这个问题的表述是值得怀疑的。

要了解原因，考虑无限的回报序列，没有开始或结束，也没有明确标识的状态。 状态可能仅由特征向量表示，这可能对于将状态彼此区分起来几乎没有作用。 作为特殊情况，所有特征向量可以是相同的。因此，实际上只有奖励序列（和行动），并且必须纯粹从这些评估表现。 怎么可能呢？一种方法是通过长时间间隔的平均奖励──这是平均奖励设置的想法。 如何使用折扣？那么，对于每个时步，我们可以衡量折扣回报。 有些回报会很小而且有些大，所以我们必须在很长的时间间隔内对它们进行平均。 在持续设置中没有开始和结束，也没有特殊的时步，因此没有其他任何事情可以做。 但是，如果你这样做，结果是折扣回报的平均值与平均回报成正比。 事实上，对于策略 \(\pi\)，折扣回报的平均值总是 \(r(\pi)/(1-\gamma)\)， 也就是说，它基本上是平均回报 \(r(\pi)\)。 特别是，平均折扣回报设置中所有策略的 排序 与平均奖励设置中的排序完全相同。 因此，折扣率 \(\gamma\) 对问题的表述没有影响。它实际上可能为 零，排名将保持不变。

这个令人惊讶的事实已在下面的框中得到证实，但基本思想可以通过对称论证来看到。 每个时步与其他步骤完全相同。通过折扣，每个奖励在某些回报中只会出现在每个位置一次。 第 \(t\) 次奖励将在第 \(t-1\) 次回报中显示为未折扣， 在第 \(t-2\) 次回报中折扣一次，在第 \(t-1000\) 次回报中折扣999次。 第 \(t\) 次奖励的权重是 \(1+\gamma+\gamma^{2}+\gamma^{3}+\cdots=1/(1-\gamma)\)。 因为所有的状态都是相同的，所以它们都由此加权， 因此回报的平均值将是此权重乘以平均奖励，或 \(r(\pi)/(1-\gamma)\)。

持续问题中折扣的无用性

也许可以通过选择一个目标来节省折扣，该目标将折扣值与策略下发生状态的分布相加：

\[\begin{split}\begin{aligned} J(\pi) &=\sum_{s} \mu_{\pi}(s) v_{\pi}^{\gamma}(s) & \text { (其中 } v_{\pi}^{\gamma} \text { 是折扣价值函数) } \\ &=\sum_{s} \mu_{\pi}(s) \sum_{a} \pi(a | s) \sum_{s^{\prime}} \sum_{r} p\left(s^{\prime}, r | s, a\right)\left[r+\gamma v_{\pi}^{\gamma}\left(s^{\prime}\right)\right] &\text {(Bellman 方程)} \\ &=r(\pi)+\sum_{s} \mu_{\pi}(s) \sum_{a} \pi(a | s) \sum_{s^{\prime}} \sum_{r} p\left(s^{\prime}, r | s, a\right) \gamma v_{\pi}^{\gamma}\left(s^{\prime}\right) &\text{(由10.7)} \\ &=r(\pi)+\gamma \sum_{s^{\prime}} v_{\pi}^{\gamma}\left(s^{\prime}\right) \sum_{s} \mu_{\pi}(s) \sum_{a} \pi(a | s) p\left(s^{\prime} | s, a\right) &\text{(由3.4)} \\ &=r(\pi)+\gamma \sum_{s^{\prime}} v_{\pi}^{\gamma}\left(s^{\prime}\right) \mu_{\pi}\left(s^{\prime}\right) &\text{(由10.8)} \\ &=r(\pi)+\gamma J(\pi) \\ &=r(\pi)+\gamma r(\pi)+\gamma^{2} J(\pi) \\ &=r(\pi)+\gamma r(\pi)+\gamma^{2} r(\pi)+\gamma^{3} r(\pi)+\cdots \\ &=\frac{1}{1-\gamma} r(\pi) \end{aligned}\end{split}\]

提出的折扣目标要求策略与未折现（平均奖励）目标相同。折扣率 \(\gamma\) 不影响排序！

此示例和框中更一般的参数表明，如果我们优化了在策略分布上的折扣值， 那么效果将与优化 未折扣 的平均奖励相同；\(\gamma\) 的实际值将无效。 这有力地表明，在函数竟是的控制问题的定义中，折扣没有任何作用。 然而，人们可以继续在解决方案中使用折扣。折扣参数 \(\gamma\) 从问题参数更改为解决方法方法参数！ 不幸的是，具有函数近似的折扣算法不会优化在策略分布上的折扣值，因此不能保证优化平均奖励。

折扣控制设置的困难的根本原因是，通过函数近似，我们已经失去了策略提升定理（第4.2节）。 如果我们改变策略以提高一个状态的折扣值，那么我们就可以保证在任何有用的意义上改善整体策略。 这种保证是我们强化学习控制方法理论的关键。随着函数近似我们失去了它！

事实上，缺乏策略提升定理也是总回合和平均奖励设置的理论空白。 一旦我们引入函数近似，我们就无法再保证任何设置的提升。 在第13章中，我们介绍了基于参数化策略的另一类强化学习算法， 并且我们有一个理论上的保证称为“策略梯度定理”，其作用与策略提升定理类似。 但是对于学习动作价值的方法，我们似乎目前没有局部改进保证（Perkins和Precup（2003）采用的方法可能提供答案的一部分）。 我们确实知道 \(\varepsilon\) -贪婪化有时可能导致低劣的策略， 因为策略可能会在好的策略之间振动而不是收敛（Gordon，1996a）。这是一个有多个开放理论问题的领域。

10.5 差分半梯度n步Sarsa

为了推广到n步自举，我们需要一个TD误差的n步版本。我们首先将n步回报（7.4）推广到其差分形式，并使用函数近似：

(12)\[G_{t : t+n} \doteq R_{t+1}-\overline{R}_{t+n-1}+\cdots+R_{t+n}-\overline{R}_{t+n-1}+\hat{q}\left(S_{t+n}, A_{t+n}, \mathbf{w}_{t+n-1}\right)\]

其中 \(\overline{R}\) 是 \(r(\pi)\) 的一个估计，\(n\geq 1\) 且 \(t+n<T\)。 如果 \(t+n \geq T\) 则我们如通常一样定义 \(G_{t : t+n} \doteq G_{t}\)。 则n步TD误差为

(13)\[\delta_{t} \doteq G_{t : t+n}-\hat{q}\left(S_{t}, A_{t}, \mathbf{w}\right)\]

之后我们可以应用我们通常的半梯度Sarsa更新（10.12）。框中给出了完整算法的伪代码。

差分半梯度n步Sarsa估计 \(\hat{q} \approx q_\pi\) 或 \(q_*\)

输入：可微分函数 \(\hat{q} : \mathcal{S} \times \mathcal{A} \times \mathbb{R}^{d} \rightarrow \mathbb{R}\)，策略 \(\pi\)

任意初始化价值函数权重 \(\mathbf{w} \in \mathbb{R}^{d}\) （比如 \(\mathbf{w}=\mathbf{0}\)）

任意初始化平均奖励估计 \(\overline{R} \in \mathbb{R}\) （比如 \(\overline{R}=0\)）

算法参数：步长 \(\alpha,\beta>0\)，正整数 \(n\)

所有存储和访问操作（\(S_t\)，\(A_t\) 和 \(R_t\)）都可以使用它们的索引 \(mod n+1\)

初始化动作 \(S_0\)，状态 \(A_0\)

对 \(t=0,1,2, \ldots\) 每步循环：

采取动作 \(A_t\)

观察和存储下一个奖励为 \(R_{t+1}\) 和下一个状态为 \(S_{t+1}\)

选择并存储动作 \(A_{t+1} \sim \pi(\cdot | S_{t+1})\) 或者关于 \(\hat{q}(S_{t+1}, \cdot, \mathbf{w})\) \(\varepsilon\) -贪婪

\(\tau \leftarrow t-n+1\) （\(\tau\) 是其估算值正在更新的时间）

如果 \(\tau>0\)：

\(\delta \leftarrow \sum_{i=\tau+1}^{\tau+n}\left(R_{i}-\overline{R}\right)+\hat{q}\left(S_{\tau+n}, A_{\tau+n}, \mathbf{w}\right)-\hat{q}\left(S_{\tau}, A_{\tau}, \mathbf{w}\right)\)

\(\overline{R} \leftarrow \overline{R}+\beta \delta\)

\(\mathbf{w} \leftarrow \mathbf{w}+\alpha \delta \nabla \hat{q}\left(S_{\tau}, A_{\tau}, \mathbf{w}\right)\)

练习10.9 在差分半梯度n步Sarsa算法中，平均奖励的步长参数 \(\beta\) 需要非常小， 以便 \(\overline{R}\) 成为平均奖励的良好长期估计。 不幸的是，\(\overline{R}\) 会因许多步骤的初始值而产生偏差，这可能会使学习变得无用。 或者，我们可以使用 \(\overline{R}\) 观察到的奖励的样本平均值。 这最初会迅速适应，但从长远来看也会缓慢适应。 随着策略的缓慢变化，\(\overline{R}\) 也会发生变化；这种长期非平稳性的可能性使得采样平均方法不适合。 实际上，平均奖励的步长参数是使用练习2.7中无偏的恒定步长技巧的理想场所。 描述上面的框中差分半梯度n步Sarsa的算法使用此技巧所需的具体变化。

10.6 总结

在本章中，我们将前一章介绍的参数化函数近似和半梯度下降的思想扩展到控制。 对于回合案例，延期是即时的，但对于持续的情况，我们必须基于最大化每个时步的 平均奖励设置 来引入全新的问题公式。 令人惊讶的是，折扣设置不能在存在近似值的情况下进行控制。在大致情况下，大多数策略不能用价值函数表示。 剩下的任意策略需要排序，标量平均奖励 \(r(\pi)\) 提供了一种有效的方法。

平均奖励公式包括价值函数的新 差分 版本，Bellman方程和TD误差，但所有这些都与旧的并行，并且概念变化很小。 对于平均奖励情况，还有一组新的并行的差分算法。

书目和历史评论

10.1 Rummery和Niranjan（1994）首次探讨了具有函数近似的半梯度Sarsa。 具有 \(\varepsilon\) -贪婪动作选择的线性半梯度Sarsa在通常意义上并不收敛， 但确实进入了最佳解决方案附近的有界区域（Gordon，1996a，2001）。 Pupcup和Perkins（2003）展示出在可微分作用选择中表现出收敛性。 可参见Perkins和Pendrith（2002）以及Melo，Meyn和Ribeiro（2008）。 陡坡汽车的例子是基于Moore（1990）研究的类似任务，但这里使用的确切形式来自Sutton（1996）。

10.2 回合n步半梯度Sarsa基于van Seijen（2016）的前向Sarsa(\(\lambda\))算法。 此处显示的实证结果是本文第二版的新内容。

10.3 已经描述了动态规划的平均奖励表述（例如，Puterman，1994）和强化学习的观点 （Mahadevan，1996；Tadepalli和Ok，1994； Bertsekas和Tsitsiklis，1996；Tsitsiklis和Van Roy，1999年）。 这里描述的算法是Schwartz（1993）引入的“R-learning”算法的在策略类比。 R-learning的名称可能是Q-learning的字母继承者，但我们更愿意将其视为学习差分或 相对 价值的参考。 Carlstr̈om和Nordstr̈om（1997）的工作提出了访问控制排队的例子。

10.4 在本文第一版出版后不久，作者对作为具有函数近似的强化学习问题的表述的限制的认识变得明显。 Singh，Jaakkola和Jordan（1994）可能是第一个在印刷品中注意到它的人。

[1]	特别地，我们使用了铺片编码软件，可从http://incompleteideas.net/tiles/tiles3.html获得， 其中 \(\text{int}=\operatorname{IHT}(4096)\) 和 \(\text{tiles}(\text{iht}, 8,[8*x/(0.5+1.2), 8*xdot/(0.07+0.07)], A)\) 得到状态 \((x，xdot)\) 和动作 \(A\) 的特征向量中的索引。

[2]	这个数据实际上来自“半梯度Sarsa(\(\lambda\))”算法，直到第12章我们都不会遇到，但是半梯度Sarsa的行为类似。