第13章 策略梯度方法¶
在本章中,我们考虑一些新内容。到目前为止,在本书中几乎所有的方法都是 动作价值方法。 他们了解了动作的价值,然后根据他们估计的行动价值选择行动 [1];如果没有动作价值估计,他们的策略甚至将不存在。 在本章中,我们考虑的方法是学习 参数化策略,该策略可以选择动作而无需咨询价值函数。 价值函数仍可用于 学习 策略参数,但动作选择不是必需的。 我们使用 \(\mathbf{\theta} \in \mathbb{R}^{d^{\prime}}\) 表示策略的参数向量。 因此假设环境在时间 \(t\) 时处于状态 \(s\),且参数为 \(\mathbf{\theta}\), 则在时间 \(t\) 采取动作 \(a\) 的概率为 \(\pi(a | s, \mathbf{\theta})={Pr}\{A_{t}=a | S_{t}=s, \mathbf{\theta}_{t}=\mathbf{\theta}\}\)。 如果一种方法也使用学习的值函数,则该值函数的权重向量将通常表示为 \(\mathbf{w} \in \mathbb{R}^{d}\), 如 \(\hat{v}(s, \mathbf{w})\) 所示。
在本章中,我们考虑基于一些基于标量性能指标 \(J(\mathbf{\theta})\) 梯度的相对于策略参数的学习策略参数的方法。 这些方法试图使性能 最大化,因此它们的更新近似 \(J\) 中的梯度 上升:
其中 \(\widehat{\nabla J\left(\mathbf{\theta}_{t}\right)} \in \mathbb{R}^{d^{\prime}}\) 是一个随机估计, 其期望近似于性能度量相对于其参数 \(\mathbf{\theta}_{t}\) 的梯度。 遵循此一般模式的所有方法,我们都称为 策略梯度方法,无论它们是否也学习近似值函数。 学习策略和值函数的近似值的方法通常称为 演员-评论家 方法,其中“演员”是指所学策略,而“评论家”是指所学习的值函数,通常是状态价值函数。 首先,我们处理回合案例,其中性能定义为参数化策略下的开始状态的值, 然后再继续考虑持续案例,其中性能定义为平均奖励率,如10.3节所述。 最后,我们能够以非常相似的形式表达两种情况的算法。
13.1 策略近似及其优势¶
在策略梯度方法中,只要 \(\pi(a|s,\boldsymbol{\theta})\) 相对于其参数是可微的, 即只要 \(\nabla \pi(a|s,\boldsymbol{\theta})\) (\(\pi(a|s,\boldsymbol{\theta})\) 相对于 \(\boldsymbol{\theta}\) 的偏导数的列向量) 存在且对于所有 \(s \in \mathcal{S}\),\(a \in \mathcal{A}(s)\) 和 \(\boldsymbol{\theta} \in \mathbb{R}^{d^{\prime}}\) 是有限的。 在实践中,为了确保探索,我们通常要求策略永远不要具有确定性 (即,对于所有 \(s\),\(a\),\(\boldsymbol{\theta}\),有 \(\pi(a | s, \boldsymbol{\theta}) \in (0,1)\))。 在本节中,我们介绍离散动作空间的最常见参数化方法,并指出其相对于动作值方法的优势。 基于策略的方法还提供了处理连续动作空间的有用方法,这将在后面的13.7节中介绍。
如果动作空间是离散的并且不是太大,那么自然和常见的一种参数化将是为每个状态-动作对形成参数化的数值偏好(preferences)。 \(h(s, a, \boldsymbol{\theta}) \in \mathbb{R}\)。 在每个状态下,具有最高偏好的动作被赋予最高的选择概率,例如,根据指数soft-max分布:
其中 \(e \approx 2.71828\) 是自然对数的底数。请注意,这里的分母是所需要的,因此每种状态下的动作概率总和为1。 我们将这种策略参数化称为 动作偏好soft-max (soft-max in action preferences)。
动作偏好本身可以任意设置。例如,它们可以由深度人工神经网络(ANN)计算,其中 \(\boldsymbol{\theta}\) 是网络所有连接权重的向量(如第16.6节中所述的AlphaGo系统)。 或者简单地,偏好可以在特征上是线性的,
使用通过第9.5节中所述的任何方法构造的特征向量 \(\mathbf{x}(s, a) \in \mathbb{R}^{d^{\prime}}\)。
根据动作偏好中的soft-max参数化策略的一个优点是,近似策略可以接近确定性策略, 而基于动作选择的 \(\varepsilon\) 贪婪总是有 \(\varepsilon\) 可能性选择随机动作。 当然,人们可以根据基于动作值的soft-max分布进行选择,但是仅此一项就无法使该策略接近确定性策略。 取而代之的是,动作值估算将收敛到其对应的真实值,这会与之相差一个有限值,转化为除0和1之外的特定概率。 如果soft-max分布包含温度参数,则温度可以随着时间的推移降低达到确定, 但是在实践中没有比我们想像的更多的先验知识,我们很难选择减少策略,甚至是初始温度。 动作偏好不同,因为它们不接近特定的值;相反,它们被驱使产生最优的随机策略。 如果最优策略是确定性的,则最优动作的偏好将无限地高于所有次优动作(如果参数化允许)。
根据动作偏好中的soft-max参数化策略的第二个优点是,它可以选择具有任意概率的动作。 在具有近似函数逼近的问题中,最佳近似策略可能是随机的。例如,在信息不完善的纸牌游戏中, 最佳玩法通常是用特定的概率来做两种不同的事情,例如在扑克中诈(bluffing)。 动作值方法没有找到随机最优策略的自然方法,而策略逼近方法却可以,如示例13.1所示。
例13.1:带有切换动作的短廊
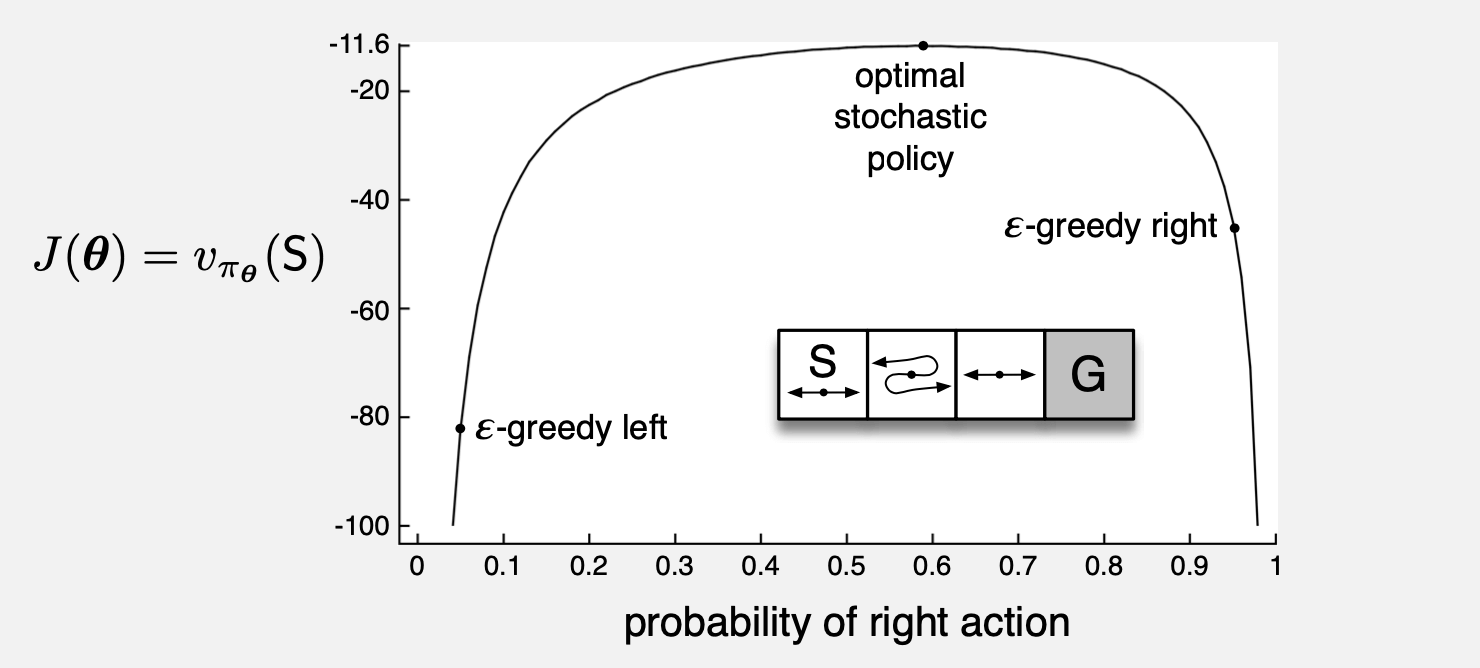
考虑下图所示的小走廊网格世界。与往常一样,奖励为每步 \(-1\)。在这三个非终结状态的每一个中,只有两个动作,即 向右 和 向左 。 这些动作在第一状态和第三状态中具有通常的结果(在第一状态中 向左 则不移动),但是在第二状态中,它们是相反的,因此右移 向左 ,左移 向右 。 问题是困难的,因为在函数近似下所有状态看起来都相同。特别地,我们为所有 \(s\) 定义 \(\mathbf{x}(s, \text { right })=[1,0]^{\top}\) 和 \(\mathbf{x}(s, \text { left })=[0,1]^{\top}\)。 具有 \(\varepsilon\) 贪婪动作选择的动作值方法被迫在两个策略之间进行选择: 在所有步骤上以高概率 \(1-\varepsilon / 2\) 选择 向右 或在所有时步上以相同的高概率选择左。 如果 \(\varepsilon=0.1\),则这两个策略达到的值(在开始状态下)分别小于 \(-44\) 和 \(-82\),如图所示。 如果一种方法可以学习选择 向右 的特定概率,则可以做得更好。最佳概率约为0.59,最后值大约为 \(-11.6\)。
相比于动作值参数化,策略参数化可能具有的最简单的优势是策略可能是一种做近似更简单的函数。 问题的策略和行动价值函数的复杂性各不相同。 对于某些来说,动作值函数更简单,因此更容易近似。对于其他,策略更简单。 在后一种情况下,基于策略的方法通常将学习得更快,并产生更好的渐近策略 (如俄罗斯方块;请参见Şimşek, Algórta和Kothiyal,2016年)。
最后,我们注意到,策略参数化的选择有时是将有关所需策略形式的先验知识注入强化学习系统的好方法。 这通常是使用基于策略的学习方法的最重要原因。
练习13.1 用你对网格世界及其动力学的知识来确定一个精确的符号表达式,以获取示例13.1中选择 向右 动作的最佳概率。