第9章 在策略预测近似方法¶
在本章中,我们开始研究强化学习中的函数近似,考虑其在从在策略数据中估计状态-价值函数的用途, 即从使用已知策略 \(\pi\) 生成的经验近似 \(v_\pi\)。 本章的新颖之处在于,近似值函数不是用表格表示, 而表示成是具有权重向量 \(\mathbf{w} \in \mathbb{R}^{d}\) 的参数化函数形式。 我们将权重向量 \(\mathbf{w}\) 的状态 \(s\) 的近似值写作 \(\hat{v}(s,\mathbf{w})\approx v_{\pi}(s)\)。 例如,\(\hat{v}\) 可能是状态特征中的线性函数,\(\mathbf{w}\) 是特征权重的向量。 更一般地,\(\hat{v}\) 可以是由多层人工神经网络计算的函数,其中 \(\mathbf{w}\) 是所有层中的连接权重的向量。 通过调整权重,网络可以实现各种不同函数中的任何一种。 或者 \(\hat{v}\) 可以是由决策树计算的函数,其中 \(\mathbf{w}\) 是定义树的分裂点和叶值的所有数字。 通常,权重的数量(\(\mathbf{w}\) 的维数)远小于状态的数量(\(d\ll|\mathcal{S}|\)), 并且改变一个权重会改变许多状态的估计值。因此,当更新单个状态时,更改会从该状态推广到许多其他状态的值。 这种 泛化 使得学习可能更强大,但也可能更难以管理和理解。
也许令人惊讶的是,将强化学习扩展到函数近似也使其适用于部分可观察到的问题,其中个体无法获得完整状态。 如果 \(\hat{v}\) 的参数化函数形式不允许估计值依赖于状态的某些方面,那么就好像这些方面是不可观察的。 实际上,本书这一部分中使用函数近似的方法的所有理论结果同样适用于部分可观察的情况。 然而,函数近似不能做的是用过去观察的记忆来增强状态表示。第17.3节简要讨论了一些可能的进一步扩展。
9.1 价值函数近似¶
本书中涉及的所有预测方法都被描述为对估计价值函数的更新,该函数将其在特定状态下的值转换为该状态的“备份值”或 更新目标。 让我们使用符号 \(s \mapsto u\) 的表示单独更新,其中 \(s\) 是更新的状态, \(u\) 是 \(s\) 的估计价值转移到的更新目标。 例如,价值预测的蒙特卡洛更新是 \(S_{t} \mapsto G_{t}\), TD(0)更新是 \(S_{t} \mapsto R_{t+1}+\gamma \hat{v}(S_{t+1}, \mathbf{w}_{t})\), n步TD更新为 \(S_{t} \mapsto G_{t:t+n}\)。在DP(动态规划)中策略评估更新, \(s\mapsto\mathbb{E}_{\pi}\left[R_{t+1}+\gamma\hat{v}(S_{t+1},\mathbf{w}_{t})|S_{t}=s\right]\), 任意状态 \(s\) 被更新,而在其他情况下,实际经验中遇到的状态 \(S_t\) 被更新。
将每个更新解释为指定价值函数的所需输入-输出行为的示例是很自然的。 从某种意义上说,更新 \(s \mapsto u\) 表示状态 \(s\) 的估计值应更像更新目标 \(u\)。 到目前为止,实际的更新是微不足道的:\(s\) 的估计值的表条目已经简单地转移到了 \(u\) 的一小部分, 并且所有其他状态的估计值保持不变。现在,我们允许任意复杂和精致方法来实现更新,并在 \(s\) 处进行更新,以便更改许多其他状态的估计值。 学习以这种方式模拟输入输出示例的机器学习方法称为 监督学习 方法,当输出是像 \(u\) 的数字时,该过程通常称为 函数近似。 函数近似方法期望接收它们试图近似的函数的期望输入-输出行为的示例。 我们使用这些方法进行价值预测,只需将每次更新的 \(s \mapsto u\) 作为训练样例传递给它们。 然后,我们将它们产生的近似函数解释为估计价值函数。
以这种方式将每个更新视为传统的训练示例使我们能够使用任何广泛的现有函数近似方法来进行价值预测。 原则上,我们可以使用任何方法进行监督学习,例如人工神经网络,决策树和各种多元回归。 然而,并非所有函数近似方法都同样适用于强化学习。最复杂的人工神经网络和统计方法都假设一个静态训练集,在其上进行多次传递。 然而,在强化学习中,学习能够在线进行,而个体与其环境或其环境模型进行交互是很重要的。 要做到这一点,需要能够从增量获取的数据中有效学习的方法。 此外,强化学习通常需要函数近似方法能够处理非平稳目标函数(随时间变化的目标函数)。 例如,在基于GPI(广义策略迭代)的控制方法中,我们经常寻求在 \(\pi\) 变化时学习 \(q_\pi\)。 即使策略保持不变,如果训练示例的目标值是通过自举方法(DP和TD学习)生成的,则它们也是非平稳的。 不能轻易处理这种非平稳性的方法不太适合强化学习。
9.2 预测目标(\(\overline{\mathrm{VE}}\))¶
到目前为止,我们尚未指定明确的预测目标。在表格的情况下,不需要连续测量预测质量,因为学习价值函数可以精确地等于真值函数。 此外,每个状态的学习价值都是分离的──一个状态的更新不受其他影响。 但是通过真正的近似,一个状态的更新会影响许多其他状态,并且不可能使所有状态的值完全正确。 假设我们有比权重更多的状态,所以使一个状态的估计更准确总是意味着让其他的不那么准确。 我们有义务说出我们最关心的状态。 我们必须指定状态分布 \(\mu(s)\geq 0,\sum_{s}\mu(s)=1\),表示我们关心每个状态 \(s\) 中的错误的程度。 通过状态 \(s\) 中的误差,我们指的是近似值 \(\hat{v}(s, \mathbf{w})\) 与 真值 \(v_\pi(s)\) 之间的差的平方。 通过 \(\mu\) 对状态空间加权,我们得到一个自然目标函数,均方误差,表示为 \(\overline{\mathrm{VE}}\):
该度量的平方根(根 \(\overline{\mathrm{VE}}\))粗略地衡量了近似值与真实值的差异,并且通常用于图中。 通常 \(\mu(s)\) 被选择为 \(s\) 中花费的时间的一部分。 在在策略训练中,这被称为 在策略分布;我们在本章中完全关注这个案例。 在持续任务中,在策略分布是 math:pi 下的固定分布。
回合任务中的在策略分布
在一个回合任务中,在策略分布略有不同,因为它取决于如何选择回合的初始状态。 设 ;math:h(s) 表示回合在每个状态 \(s\) 中开始的概率, \(\eta(s)\) 表示在一个回合中状态 \(s\) 中平均花费的时间步数。 如果回合以 \(s\) 开头,或者如果从之前的状态 \(\overline{s}\) 转换为 \(s\),则花费时间在状态 \(s\) 中:
可以针对预期的访问次数 \(\eta(s)\) 求解该方程组。 然后,在策略分布是每个状态所花费的时间的一小部分,标准化和为一:
这是没有折扣的自然选择。如果存在折扣(\(\gamma<1\)),则应将其视为终止形式, 这可以简单通过在(9.2)的第二项中包含因子 \(\gamma\) 来完成。
这两种情况,即持续的和回合的,表现相似,但近似时必须在形式分析中单独处理, 正如我们将在本书的这一部分中反复看到的那样。这完成了学习目标的规范。
目前还不完全清楚 \(\overline{\mathrm{VE}}\) 是加强学习的正确性能目标。 请记住,我们的最终目的──我们学习价值函数的原因──是找到更好的策略。 用于此目的的最佳价值函数不一定是最小化 \(\overline{\mathrm{VE}}\) 的最佳值。 然而,目前尚不清楚价值预测的更有用的替代目标是什么。目前,我们将专注于 \(\overline{\mathrm{VE}}\)。
就 \(\overline{\mathrm{VE}}\) 而言,理想的目标是找到一个 全局最优值, 一个权重向量 \(\mathbf{w}^{*}\),对于所有可能的 \(\mathbf{w}\), \(\overline{\mathrm{VE}}(\mathbf{w}^{*})\leq\overline{\mathrm{VE}}(\mathbf{w})\)。 对于诸如线性函数近似器之类的简单函数逼近器,有时可以实现这一目标, 但对于诸如人工神经网络和决策树之类的复杂函数近似器来说很少是可能的。 除此之外,复杂函数近似器可以寻求收敛到 局部最优,一个权重向量 \(\mathbf{w}\), 对于 \(\mathbf{w}^{*}\) 的某些邻域中的所有 \(\mathbf{w}\) 满足 \(\overline{\mathrm{VE}}(\mathbf{w}^{*})\leq\overline{\mathrm{VE}}(\mathbf{w})\)。 虽然这种保证只是稍微让人放心,但对于非线性函数近似器来说,它通常是最好的,而且通常它就足够了。 尽管如此,对于许多对强化学习感兴趣的情况,并不能保证收敛到最佳,甚至在最佳的有界距离内。 事实上,有些方法可能会出现发散,其 \(\overline{\mathrm{VE}}\) 极限趋于无穷。
在前两节中,我们概述了一个框架,用于将价值预测的各种强化学习方法与各种函数近似方法相结合,使用前者的更新为后者生成训练样本。 我们还描述了这些方法可能希望最小化的 \(\overline{\mathrm{VE}}\) 性能测量。 可能的函数近似方法的范围太大以至于不能覆盖所有方法,并且无论如何对其中的大多数方法进行可靠的评估或推荐知之甚少。 必要时,我们只考虑几种可能性。在本章的剩余部分,我们将重点放在基于梯度原理的函数近似方法,特别是线性梯度下降方法上。 我们关注这些方法的部分原因是因为我们认为这些方法特别有前途,因为它们揭示了关键的理论问题,同时也因为它们很简单,而且我们的空间有限。
9.3 随机梯度和半梯度方法¶
我们现在详细地开发一类用于价值预测中的函数近似的学习方法,这些方法基于随机梯度下降(SGD)。 SGD方法是所有函数近似方法中使用最广泛的方法之一,尤其适用于在线强化学习。
在梯度下降方法中,权重向量是具有固定数量的实值分量的 列向量 \(\mathbf{w} \doteq(w_{1}, w_{2}, \ldots, w_{d})^{\top}\) [1], 近似值函数 \(\hat{v}(s, \mathbf{w})\) 是 所有 \(s\in\mathcal{S}\) 的 \(\mathbf{w}\) 的可微函数。 我们将在一系列离散时间 \(t = 0,1,2,3,\dots,\) 的每一个中更新 \(\mathbf{w}\), 因此我们需要符号 \(\mathbf{w}_t\) 表示每一步的权重向量。 现在,让我们假设,在每一步,我们都观察到一个新的样例 \(S_{t} \mapsto v_{\pi}\left(S_{t}\right)\) 由一个(可能是随机选择的)状态 \(S_t\) 和它在策略下的真实值组成。 这些状态可能是与环境交互的连续状态,但是现在我们不这么认为。 即使我们给出了每个 \(S_t\) 的精确而正确的价值 \(v_{\pi}\left(S_{t}\right)\), 这仍然存在一个难题,因为我们的函数近似器具有有限的资源并因此具有有限的进精度(resolution)。 特别是,通常没有 \(\mathbf{w}\) 能够使所有状态,甚至所有样例都完全正确。 此外,我们必须推广到未出现在示例中的所有其他状态。
我们假设状态出现在具有相同分布 \(\mu\) 的样例中, 我们试图通过它来最小化由(9.1)给出的 \(\overline{\mathrm{VE}}\)。 在这种情况下,一个好的策略是尽量减少观察到的样例的错误。 随机梯度下降 (SGD)方法通过在每个样例之后将权重向量向最大程度地减少该示例中的误差的方向少量调整来实现此目的:
其中 \(\alpha\) 是正步长参数,对于作为向量函数(这里是 \(\mathbf{w}\))的 任何标量表达式 \(f(\mathbf{w})\),\(\nabla f(\mathbf{w})\) 定义为关于向量分量 表达式的偏导数的列向量,向量分量为:
该导数向量是 math:f 相对于 \(\mathbf{w}\) 的梯度。SGD方法是“梯度下降”方法, 因为 \(\mathbf{w}_t\) 中的整个步长与示例的平方误差(9.4)的负梯度成比例。这是误差下降最快的方向。 当像这儿仅在单个可能是随机选择的样例上完成更新时,梯度下降方法被称为“随机”。 在许多样例中,采取小步,总体效果是最小化如VE的平均性能测量。
可能不会立即明白为什么SGD在梯度方向上只迈出一小步。难道我们不能一直朝这个方向移动并完全消除样例中的误差吗? 在许多情况下,这可以做到,但通常是不可取的。请记住,我们不会寻找或期望找到一个对所有状态都没有误差的价值函数, 而只是一个平衡不同状态误差的近似值。如果我们在一个步骤中完全纠正每个样例,那么我们就找不到这样的平衡。 事实上,SGD方法的收敛结果假设 \(\alpha\) 随着时间的推移而减少。 如果它以满足标准随机近似条件(2.7)的方式减小,则SGD方法(9.5)保证收敛到局部最优。
我们现在转向第 \(t\) 个训练样例 \(S_{t} \mapsto U_{t}\) 的目标输出 (此处表示为 \(U_{t}\in\mathbb{R}\))不是真值 \(v_\pi(S_t)\) 而是一些(可能是随机的)近似的情况。 例如,\(U_{t}\) 可能是 \(v_\pi(S_t)\) 的噪声损坏版本, 或者它可能是使用上一节中提到的 \(\hat{v}\) 的自举目标之一。 在这些情况下,我们无法执行精确更新(9.5),因为 \(v_\pi(S_t)\) 是未知的, 但我们可以通过用 \(U_t\) 代替 \(v_\pi(S_t)\) 来近似它。 这产生了以下用于状态价值预测的一般SGD方法:
如果 \(U_t\) 是无偏估计,即,如果对于每个 \(t\) 有 \(\mathbb{E}\left[U_{t} | S_{t}=s\right]=v_{\pi}(S_{t})\), 则 \(\mathbf{w}_t\) 保证对于减小的 \(\alpha\) 在通常的随机近似条件(2.7)下收敛到局部最优值。
例如,假设示例中的状态是通过使用策略 \(\pi\) 与环境交互(或模拟交互)生成的状态。 因为状态的真实值是跟随它的回报的预期值, 所以蒙特卡洛目标 \(U_{t}\doteq G_{t}\) 根据定义是 \(v_\pi(S_t)\) 的无偏估计。 通过这种选择,一般SGD方法(9.7)收敛于 \(v_\pi(S_t)\) 的局部最佳近似。 因此,蒙特卡洛状态价值预测的梯度下降版本保证找到局部最优解。完整算法的伪代码如下框所示。
梯度蒙特卡罗算法估计 \(\hat{v} \approx v_{\pi}\)
输入:要评估的策略 \(\pi\)。
输入:可微分函数 \(\hat{v} : \mathcal{S} \times \mathbb{R}^{d} \rightarrow \mathbb{R}\)
算法参数:步长 \(\alpha>0\)
任意初始化价值函数权重 \(\mathbf{w} \in \mathbb{R}^{d}\) (例如,\(\mathbf{w}=\mathbf{0}\))
一直循环(对每一个回合):
使用 \(\pi\) 生成一个回合 \(S_{0}, A_{0}, R_{1}, S_{1}, A_{1}, \ldots, R_{T}, S_{T}\)
对回合的每一步循环,\(t=0,1, \ldots, T-1\):
\(\mathbf{w} \leftarrow \mathbf{w}+\alpha\left[G_{t}-\hat{v}(S_{t}, \mathbf{w})\right] \nabla \hat{v}(S_{t}, \mathbf{w})\)
如果将 \(v_\pi(S_t)\) 的自举估计用作(9.7)中的目标 \(U_t\),则不能获得相同的保证。 自举目标如n步回报 \(G_{t : t+n}\) 或DP目标 \(\sum_{a,s^{\prime},r}\pi(a | S_{t}) p(s^{\prime}, r | S_{t}, a)\left[r+\gamma \hat{v}(s^{\prime}, \mathbf{w}_{t})\right]\) 全部依赖关于权重向量 \(\mathbf{w}_t\) 的当前值,这意味着它们将被偏置并且它们将不会产生真正的梯度下降方法。 一种看待这一点的方法是从(9.4)到(9.5)的关键步骤依赖于目标独立于 \(\mathbf{w}_t\)。 如果使用自举估计代替 \(v_\pi(S_t)\),则该步骤无效。自举方法实际上不是真正的梯度下降的实例(Barnard,1993)。 它们考虑了改变权重向量 \(\mathbf{w}_t\) 对估计的影响,但忽略了它对目标的影响。 它们只包括渐变的一部分,因此,我们将它们称为 半梯度方法。
尽管半梯度(自举)方法不像梯度方法那样稳健地收敛,但它们在重要情况下可靠地收敛,例如下一节中讨论的线性情况。 而且,它们提供了重要的优点,使它们通常是明显优选的。 这样做的一个原因是它们通常能够显着加快学习速度,正如我们在第6章和第7章中看到的那样。 另一个原因是它们使学习能够连续和在线,而无需等待回合的结束。这使它们能够用于持续的问题并提供计算优势。 一种原型半梯度方法是半梯度TD(0), 其使用 \(U_{t} \doteq R_{t+1}+\gamma \hat{v}(S_{t+1}, \mathbf{w})\) 作为其目标。 下面的框中给出了该方法的完整伪代码。
半梯度TD(0)估计 \(\hat{v} \approx v_{\pi}\)
输入:要评估的策略 \(\pi\)。
输入:可微分函数 \(\hat{v} : \mathcal{S}^{+} \times \mathbb{R}^{d} \rightarrow \mathbb{R}\) 使得 \(\hat{v}(\text{终止}, \cdot)=0\)
算法参数:步长 \(\alpha>0\)
任意初始化价值函数权重 \(\mathbf{w} \in \mathbb{R}^{d}\) (例如,\(\mathbf{w}=\mathbf{0}\))
一直循环(对每一个回合):
初始化 \(S\)
对回合的每一步循环:
选择 \(A \sim \pi(\cdot | S)\)
采取动作 \(A\),观察 \(R\),\(S^{\prime}\)
\(\mathbf{w} \leftarrow \mathbf{w}+\alpha\left[R+\gamma \hat{v}\left(S^{\prime}, \mathbf{w}\right)-\hat{v}(S, \mathbf{w})\right] \nabla \hat{v}(S, \mathbf{w})\)
\(S \leftarrow S^{\prime}\)
直到 \(S\) 终止
状态 聚合 是泛化函数近似的简单形式,其中状态被分组在一起,每个组具有一个估计值(权重向量 \(\mathbf{w}\) 的一个分量)。 状态的值被估计为其组的分量,并且当状态被更新时,仅更新该分量。状态聚合是SGD(9.7)的特例, 其中梯度 \(\nabla \hat{v}(S_{t}, \mathbf{w}_{t})\) 对于 \(S_t\) 的分量为1,对于其他成分为0。
例9.1:1000状态随机行走的状态聚合 考虑1000状态版本的随机行走任务(示例6.2和7.1)。 状态从1到1000,从左到右编号,并且所有回合在中心附近状态500开始。 状态转换从当前状态到其左边的100个邻近状态之一,或者其左边的100个邻近状态之一,都具有相同的概率。 当然,如果当前状态接近边缘,那么在它的那一侧可能少于100个邻居。 在这种情况下,进入那些丢失的邻居的所有概率都会进入在那一侧终止的概率 (因此,状态1有0.5的机会在左边终止,而状态950有0.25的机会在右侧终止)。 像往常一样,左边的终止产生 \(-1\) 的奖励,右边的终止产生 \(+1\) 的奖励。 所有其他过渡奖励都为零。我们在本节中将此任务用作运行示例。
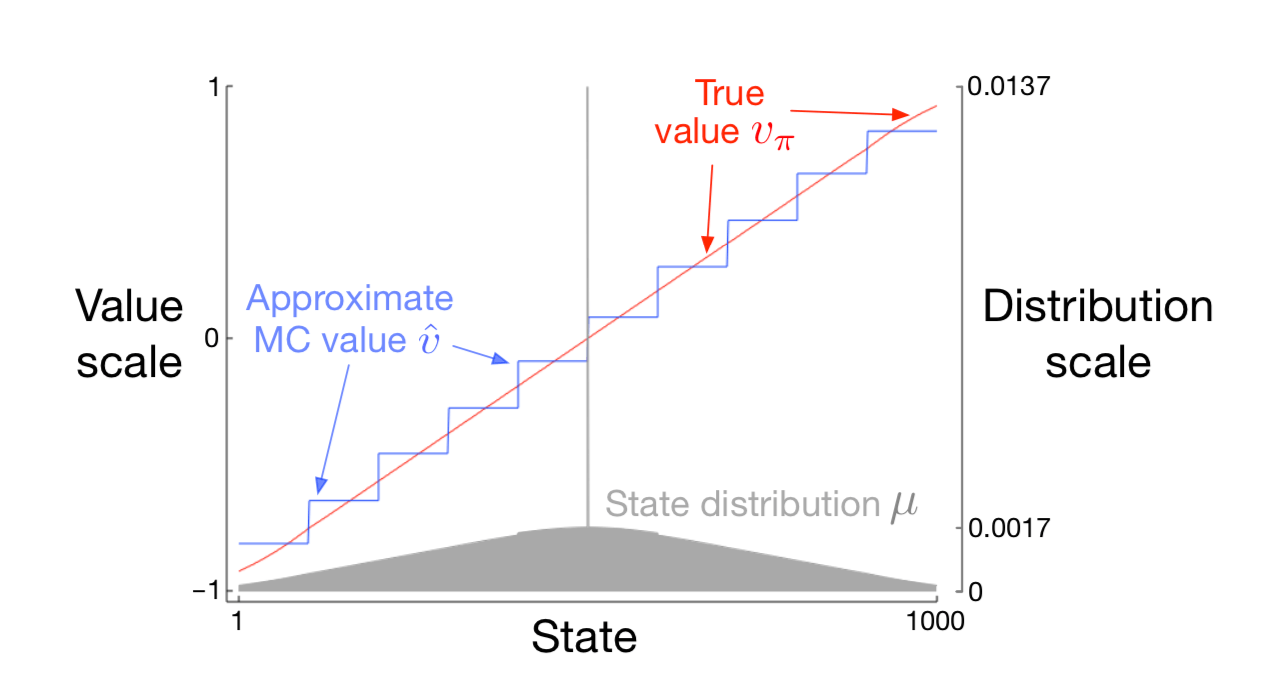
图9.1: 使用梯度蒙特卡罗算法对1000状态随机行走任务进行状态聚合的函数近似。
图9.1显示了此任务的真值函数 \(v_\pi\)。它几乎是一条直线,每端最后100个状态向水平方向略微弯曲。 图还显示了梯度蒙特卡罗算法通过状态聚合学习的最终近似价值函数, 此状态聚合具有步长为 \(\alpha=2×10^{}-5\) 的100,000个回合。 对于状态聚合,1000个状态被分成10组,每组100个状态(即,状态1-100是一组,状态101-200是另一组,等等)。 图中所示的阶梯效应是典型的状态聚合;在每个组中,近似值是恒定的,并且它从一个组突然改变到下一个组。 这些近似值接近 \(\overline{\mathrm{VE}}\) 的全局最小值(9.1)。
通过参考该任务的状态分布 \(\mu\),可以最好地理解近似价值的一些细节,如图的下部所示,标度在右侧。 位于中心的状态500是每个回合的第一个状态,但很少再次访问。平均而言,约有1.37%的时间步花费在开始状态。 从开始状态开始一步到达的状态是访问次数最多的状态,其中每个步骤花费大约0.17%的时间步。 从那里 \(\mu\) 几乎线性地下降,在极端状态1和1000处达到约0.0147%。 分布的最明显效果是在最左边的组上,其值明显偏移到高于组内状态的真实值的未加权平均值,以及在最右边的小组,其价值明显向低的方向移动。 这是由于这些区域中的状态在权重上具有最大的不对称性 \(\mu\)。 例如,在最左边的组中,状态100的加权比状态1强3倍以上。因此,对组的估计偏向于状态100的真实值,其高于状态1的真实值。
9.4 线性方法¶
函数近似的一个最重要的特殊情况是其中近似函数 \(\hat{v}(\cdot, \mathbf{w})\) 是 权重向量 \(\mathbf{w}\) 的线性函数。对应于每个状态 \(s\),存在实值向量 \(\mathbf{x}(s) \doteq(x_{1}(s), x_{2}(s), \ldots, x_{d}(s))^{\top}\), 具有与 \(\mathbf{w}\) 相同数量的分量。 线性方法通过 \(\mathbf{w}\) 和 \(\mathbf{x}(s)\) 之间的内积近似状态值函数:
在这种情况下,近似价值函数被称为 权重线性(linear in the weights),或简单地称为 线性。
向量 \(\mathbf{x}(s)\) 被称为表示状态 \(s\) 的 特征向量。 \(\mathbf{x}(s)\) 的每个分量 \(x_{i}(s)\) 是 函数 \(x_{i}:\mathcal{S}\rightarrow\mathbb{R}\) 的值。 我们将一个 特征 视为这些函数之一的整体,我们将状态 \(s\) 的一个特征。 对于线性方法,特征是 基函数,因为它们形成近似函数集的线性基。 构造表示状态的 \(d\) 维特征向量与选择一组 \(d\) 基函数相同。 可以用许多不同的方式定义特征;我们将在下一节中介绍几种可能。
很自然地可以使用SGD更新处理线性函数近似。在这种情况下,近似价值函数相对于 \(\mathbf{w}\) 的梯度是
因此,在线性情况下,一般SGD更新(9.7)简化为一种特别简单的形式:
因为它非常简单,线性SGD情况是最有利于数学分析的情况之一。 几乎所有类型的学习系统的有用收敛结果都是线性(或简单)函数近似方法。
特别是,在线性情况下,只有一个最优(或者,在简并情况下,一组同样良好的最优), 因此任何保证收敛到或接近局部最优的方法都会自动保证收敛到或接近全局最优。 例如,如果根据通常条件 \(\alpha\) 随着时间减小, 则在前一部分中呈现的梯度蒙特卡罗算法收敛于线性函数近似下的 \(\overline{\mathrm{VE}}\) 的全局最优。
上一节中介绍的半梯度TD(0)算法也收敛于线性函数近似,但这并不符合SGD的一般结果;一个单独的定理是必要的。 收敛到的权重向量也不是全局最优值,而是接近局部最优值的点。更详细地考虑这一重要案例是有用的,特别是对于持续情况。 每个时间 \(t\) 的更新是
这里我们使用了符号缩写 \(\mathbf{x}_{t}=\mathbf{x}\left(S_{t}\right)\)。 一旦系统达到稳定状态,对于任何给定的 \(\mathbf{w}_t\),下一个权重向量的期望可以写成:
其中
从(9.10)可以清楚地看出,如果系统收敛,它必须收敛到权重向量 \(\mathbf{W}_{\mathrm{TD}}\)
该数量称为 TD固定点。事实上,线性半梯度TD(0)收敛到这一点。在框中给出了一些证明其收敛性的理论,以及上述逆的存在性。
线性TD(0)的收敛性证明
什么属性确保线性TD(0)算法(9.9)的收敛?通过重写(9.10)可以获得一些见解
注意到矩阵 \(\mathbf{A}\) 乘以权重向量 \(\mathbf{w}_t\) 而不是 \(\mathbf{b}\); 只有 \(\mathbf{A}\) 对收敛很重要。 为了发展直觉,考虑 \(\mathbf{A}\) 是对角矩阵的特殊情况。如果任何对角元素为负, 则 \(\mathbf{I}-\alpha \mathbf{A}\) 的对应对角元素将大于1, 并且 \(\mathbf{w}_t\) 的相应分量将被放大,如果继续则将导致发散。 另一方面,如果 \(\mathbf{A}\) 的对角线元素都是正的,那么可以选择 \(\alpha\) 小于它们中的最大值, 使得 \(\mathbf{I}-\alpha \mathbf{A}\) 是对角矩阵,所有对角线元素在0和1之间。 在这种情况下,第一个更新期限趋于缩小 \(\mathbf{w}_t\),并确保稳定性。 通常,无论何时 \(\mathbf{A}\) 为 正定 时, 意味着对于任何实数向量 \(y \neq 0\),\(y^{\top} \mathbf{A} y>0\),\(\mathbf{w}_t\) 将减小到零。 正定性也确保存在逆 \(\mathbf{A}^{-1}\)。
对于线性TD(0),在 \(\gamma<1\) 的连续情况下,\(\mathbf{A}\) 矩阵(9.11)可以写为:
其中 \(\mu(s)\) 是 \(\pi\) 下的平稳分布, \(p\left(s^{\prime} | s\right)\) 是在策略 \(\pi\) 下从 \(s\) 过渡到 \(s^{\prime}\) 的概率, \(\mathbf{P}\) 是这些概率的 \(|\mathcal{S}|\times|\mathcal{S}|\) 矩阵, \(\mathbf{D}\) 是 \(|\mathcal{S}|\times|\mathcal{S}|\) 对角线矩阵,其对角线上有 \(\mu(s)\), \(\mathbf{X}\) 是 \(|\mathcal{S}|\times d\) 矩阵,其中 \(\mathbf{x}(s)\) 为行。 从这里可以清楚地看出,内矩阵 \(\mathbf{D}(\mathbf{I}-\gamma \mathbf{P})\) 是确定 \(\mathbf{A}\) 的正定性的关键。
对于这种形式的关键矩阵(key matrix),如果所有列的总和为非负数,则确定是正定的。 Sutton(1988,p.27)基于两个先前建立的定理证明了这一点。 一个定理说,当且仅当对称矩阵 \(\mathbf{S}=\mathbf{M}+\mathbf{M}^{\top}\) 是正定时, 任何矩阵 \(\mathbf{M}\) 都是正定的(Sutton 1988,附录)。 第二个定理说任何对称实矩阵 \(\mathbf{S}\) 是正定的, 如果它的所有对角线条目都是正的并且大于相应的非对角线条目的绝对值之和(Varga 1962,第23页)。 对于我们的关键矩阵 \(\mathbf{D}(\mathbf{I}-\gamma \mathbf{P})\), 对角线条目是正的,非对角线条目是负的,所以我们要显示的是每个行和加上相应的列和是正的。 行和都是正数,因为 \(\mathbf{P}\) 是一个随机矩阵且 \(\gamma<1\)。因此,它只是表明列和是非负的。 注意,任何矩阵 \(\mathbf{M}\) 的列和的行向量可以写为 \(\mathbf{1}^{\top} \mathbf{M}\), 其中 \(\mathbf{1}\) 是所有分量等于1的列向量。 令 \(\mathbf{\mu}\) 表示 \(\mu(s)\) 的 \(|\mathcal{S}|\) -向量, 其中 \(\mathbf{\mu}=\mathbf{P}^{\top} \mathbf{\mu}\),因为 \(\mu\) 是固定分布。 然后,我们的关键矩阵的列总和是:
所有分量都是正的。因此,关键矩阵及其 \(\mathbf{A}\) 矩阵是正定的,并且在策略TD(0)是稳定的。 (需要附加条件和随时间推移减少 \(\alpha\) 的时间表来证明收敛概率为1。)
在TD固定点,已经证明(在持续情况下) \(\overline{\mathrm{VE}}\) 在最低可能误差的有限扩展内:
也就是说,TD方法的渐近误差不超过最小可能误差的 \(\frac{1}{1-\gamma}\) 倍,这是通过蒙特卡罗方法达到的极限值。 因为 \(\gamma\) 通常接近1,所以这个扩展因子可能非常大,因此TD方法的渐近性能存在很大的潜在损失。 另一方面,回想一下,与蒙特卡罗方法相比,TD方法的方差通常大大减少,因此更快,正如我们在第6章和第7章中看到的那样。 哪种方法最好取决于近似和问题的性质,以及学习的持续时间。
类似于(9.14)的约束也适用于其他在策略自举方法。例如,线性半梯度DP(等式9.7 \(U_{t}\doteq\sum_a\pi(a|S_t)\sum_{s^{\prime},r}p(s^{\prime},r|S_t,a)[r+\gamma\hat{v}(s^{\prime},\mathbf{w}_{t})]\)) 根据在策略分布进行更新也将收敛到TD固定点。一步半梯度 动作价值 方法, 例如下一章中介绍的半梯度Sarsa(0)会收敛到类似的固定点和类似的边界。 对于回合任务,存在一个稍微不同但相关的界限(参见Bertsekas和Tsitsiklis,1996)。 步长参数的奖励,特征和减少也有一些技术条件,我们在此省略。 完整的细节可以在原始论文中找到(Tsitsiklis和Van Roy,1997)。
这些收敛结果的关键是根据在策略分布更新状态。对于其他更新分布,使用函数近似的自举方法实际上可能会发散到无穷大。 第11章给出了这方面的例子以及对可能的解决方法的讨论。
例9.2:1000个状态随机行走中的自举 状态聚合是线性函数近似的一种特殊情况, 所以让我们回到1000个状态随机行走来说明本章所做的一些观察。 图9.2的左侧面板显示了使用与例9.1中相同的状态聚合,通过半梯度TD(0)算法(9.3节)学习的最终价值函数。 我们看到近似渐近的TD近似确实比图9.1中所示的蒙特卡罗近似的真实值更远。
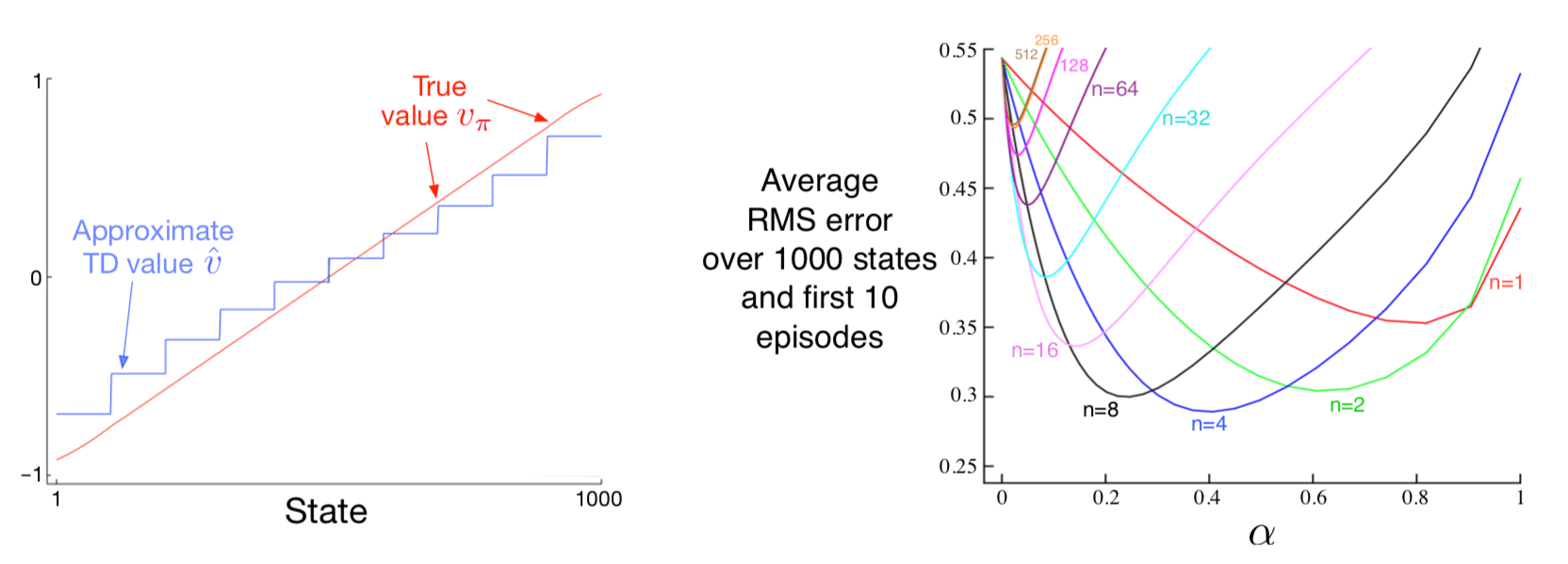
图9.2: 在1000个状态随机行走任务上使用状态聚合进行自举。 左图:半梯度TD的渐近值比图9.1中的渐近蒙特卡罗值差。 右图:具有状态聚合的n步方法的性能与具有表格表示的方法非常相似(参见图7.2)。 这些数据是100次运行的平均值。
然而,TD方法在学习速率方面保留了很大的潜在优势,并且推广了蒙特卡罗方法,正如我们在第7章中用n步TD方法完全研究的那样。 图9.2的右图显示了采用n步半梯度TD方法的结果在1000状态随机行走上使用状态聚合,这与我们之前使用表格方法和19个状态随机行走走获得的状态非常相似(图7.2)。 为了获得这种定量相似的结果,我们将状态聚合切换为20组,每组50个状态。然后,这20个小组在数量上接近表格问题的19个状态。 特别是,回想一下状态转换是向左或向右的100个状态。然后典型的转换将是向右或向左的50个状态,这在数量上类似于19状态表格系统的单状态转换。 为了完成匹配,我们在这里使用相同的性能度量──在所有状态和前10回合中的RMS误差的未加权平均值── 而不是 \(\overline{\mathrm{VE}}\) 目标,否则在使用函数近似时更合适。
在上面的例子中使用的半梯度n步TD算法是第7章中给出的表格n步TD算法对半梯度函数近似的自然扩展。伪代码在下面的框中给出。
n步半梯度TD估计 \(\hat{v} \approx v_{\pi}\)
输入:要评估的策略 \(\pi\)。
输入:可微分函数 \(\hat{v} : \mathcal{S}^{+} \times \mathbb{R}^{d} \rightarrow \mathbb{R}\) 使得 \(\hat{v}(\text{终止}, \cdot)=0\)
算法参数:步长 \(\alpha>0\),正整数 \(n\)
任意初始化价值函数权重 \(\mathbf{w}\) (例如,\(\mathbf{w}=\mathbf{0}\))
所有存储和访问操作(\(S_{t+1}\) 和 \(R_{t+1}\))都可以使用它们的索引 \(mod n+1\)
对每一个回合一直循环:
初始化并存储 \(S_0 \ne \text{终止}\)
\(T \leftarrow \infty\)
\(t=0,1,2, \ldots\) 循环:
如果 \(t<T\) 则:
根据 \(\pi(\cdot|S_t)\) 采取行动
观察并将下一个奖励存储为 \(R_{t+1}\),将下一个状态存储为 \(S_{t+1}\)
如果 \(S_{t+1}\) 终止,则 \(T \leftarrow t+1\)
\(\tau \leftarrow t - n + 1\) (\(\tau\) 是状态估计正在更新的时间)
如果 \(\tau \geq 0\):
\(G \leftarrow \sum_{i=\tau+1}^{\min (\tau+n, T)} \gamma^{i-\tau-1} R_{i}\)
如果 \(\tau + n < T\), 则 \(G \leftarrow G+\gamma^{n} \hat{v}\left(S_{\tau+n}, \mathbf{w}\right)\) \(\quad\quad\quad\) \(\left(G_{\tau : \tau+n}\right)\)
\(\mathbf{w} \leftarrow \mathbf{w}+\alpha\left[G-\hat{v}\left(S_{\tau}, \mathbf{w}\right)\right] \nabla \hat{v}\left(S_{\tau}, \mathbf{w}\right)\)
直到 \(\tau = T - 1\)
类似于(7.2),这个算法的关键方程是
其中n步回报从(7.1)推广到
练习9.1 展示本书第一部分中介绍的表格方法是线性函数近似的一种特殊情况。特征向量是什么?
9.5 线性方法的特征构造¶
线性方法因其收敛性保证而很有意思,但也因为在实践中它们在数据和计算方面都非常有效。 这是否如此关键取决于如何用特征来表示状态,我们在这一大部分中进行了研究。 选择适合任务的特征是将先前领域知识添加到强化学习系统的重要方法。 直观地,这些特征应该对应于状态空间的各个方面,沿着这些方面可以适用泛化。 例如,如果我们对几何对象进行评估,我们可能希望为每种可能的形状,颜色,大小或功能提供特征。 如果我们重视移动机器人的状态,那么我们可能希望获得位置,剩余电池电量,最近的声纳读数等功能。
线性形式的限制是它不能考虑特征之间的任何相互作用,例如特征 \(i\) 的存在仅在缺少特征 \(j\) 时才是好的。 例如,在杆平衡任务(例3.4)中,高角速度可以是好的也可以是坏的,取决于角度。如 果角度很高,那么高角速度意味着即将发生坠落的危险──一种不好的状态,而如果角度较低,那么高角速度意味着杆本身正好──一个良好的状态。 如果其特征针对角度和角速度单独编码,则线性值函数不能表示这一点。相反,或者另外,它需要用于这两个基础状态维度的组合的特征。 在以下小节中,我们考虑了许多种一般的方法。
9.5.1 多项式¶
许多问题的状态最初表示为数字,例如杆平衡任务(例3.4)中的位置和速度, 杰克汽车租赁问题(例4.2)中每个汽车的数量,或赌徒问题(例4.3)中赌徒的资本。 在这些类型的问题中,强化学习的函数近似与常见的插值和回归任务有很多共同之处。 通常用于插值和回归的各种特征族也可用于强化学习。多项式构成了用于插值和回归的最简单的特征系列之一。 虽然我们在这里讨论的基本多项式特征不像强化学习中的其他类型的特征那样有效,但它们是一个很好的介绍,因为它们简单而且熟悉。
例如,假设强化学习问题具有两个数值维度的状态。对于单个代表状态 \(s\), 让它的两个数字是 \(s_{1} \in \mathbb{R}\) 和 \(s_{2} \in \mathbb{R}\)。 你可以选择仅通过它的两个状态维度来表示 \(s\),这样 \(\mathbf{x}(s)=(s_1,s_2)^{\top}\), 但是你无法考虑这些维度之间的任何相互作用。另外,如果 \(s_1\) 和 \(s_2\) 都为零,那么近似值也必须为零。 通过用四维特征向量 \(\mathbf{x}(s)=(1,s_1,s_2,s_1 s_2)^{\top}\), 可以克服这两个限制。初始的 \(1\) 特征允许在原始状态编号中表示仿射函数,最后的乘积特征 \(s_1 s_2\) 允许考虑交互。 或者你可以选择使用更高维的特征向量,如 \(\mathbf{x}(s)=(1, s_{1}, s_{2}, s_{1} s_{2}, s_{1}^{2}, s_{2}^{2}, s_{1} s_{2}^{2}, s_{1}^{2} s_{2}, s_{1}^{2} s_{2}^{2})^{\top}\) 来考虑更复杂的交互。这样的特征向量使近似成为状态数的任意二次函数──即使近似在必须学习的权重中仍然是线性的。 将这个例子从 \(2\) 个数到 \(k\) 个数推广,我们可以表示问题的状态维度之间的高度复杂的相互作用:
注解
假设每个状态 \(s\) 对应于 \(k\) 个数,\(s_1,s_2,\ldots,s_k\),每个 \(s_{i} \in \mathbb{R}\)。 对于这个 \(k\) 维状态空间,每个有阶-n(order-n)多项式基特征 \(x_i\) 可以写为
其中每个 \(c_{i,j}\) 是集合 \(\{0,1, \ldots, n\}\) 中的整数,\(n>0\)。 这些特征构成维数 \(k\) 的阶-n多项式基,其中包含 \((n+1)^k\) 个不同的特征。
高阶多项式基允许更准确地近似更复杂的函数。 但是因为阶-n多项式基中的特征数量随自然状态空间的维数 \(k\) 呈指数增长(如果 \(n>0\)), 通常需要选择它们的子集用于函数近似。这可以使用关于要近似的函数的性质的先验信念来完成, 并且可以调整为多项式回归开发的一些自动选择方法以处理强化学习的增量和非平稳性质。
练习9.2 为什么(9.17)为维度 \(k\) 定义 \((n+1)^k\) 个不同的特征?
练习9.2 什么 \(n\) 和 \(c_{i,j}\) 产生特征向量 \(\mathbf{x}(s)=(1, s_{1}, s_{2}, s_{1} s_{2}, s_{1}^{2}, s_{2}^{2}, s_{1} s_{2}^{2}, s_{1}^{2} s_{2}, s_{1}^{2} s_{2}^{2})^{\top}\) ?
9.5.2 傅立叶基¶
另一种线性函数近似方法基于历时(time-honored)傅立叶级数,其表示周期函数为不同频率的正弦和余弦基函数(特征)的加权和。 (如果 \(f(x)=f(x+\tau)\) 对于所有 \(x\) 和一些周期 \(\tau\) 成立, 则函数 \(f\) 是周期函数。) 傅立叶级数和更一般的傅立叶变换在应用科学中被广泛使用,部分原因是如果要近似的函数是已知的, 基函数权重由简单公式给出,并且,具有足够的基函数,基本上任何函数都可以根据需要精确地近似。 在强化学习中,要近似的函数是未知的,傅里叶基函数是有意义的,因为它们易于使用并且可以在一系列强化学习问题中表现良好。
首先考虑一维情况。具有周期 \(\tau\) 的一维函数的通常傅立叶级数表示为正弦和余弦函数的线性组合的函数, 每个函数周期性地均衡分割 \(\tau\) 的周期(换句话说,其频率是整数乘以基频 \(1/\tau\))。 但是如果你对近似有界区间定义的非周期函数感兴趣,那么你可以使用这些傅里叶基特征,并将 \(\tau\) 设置为区间的长度。 因此,感兴趣的函数只是正弦和余弦特征的周期线性组合的一个周期。
此外,如果将 \(\tau\) 设置为感兴趣区间长度的两倍并将注意力限制在半区间 \([0,\tau/2]\) 的近似值上, 则可以仅使用余弦特征。这是可能的,因为你可以只用余弦基表示任何 偶 函数,即任何与原点对称的函数。 因此,半周期 \([0,\tau/2]\) 上的任何函数都可以根据需要用足够的余弦特征近似。 (说“任何函数”并不完全正确,因为函数必须在数学上表现良好,但我们在这里省略了这个技术性。) 或者,可以使用正弦特征,其线性组合总是 奇 函数,是关于原点反对称的函数。 但通常更好的是保持余弦特征,因为“半偶数”函数往往比“半奇”函数更容易近似,因为后者在原点通常是不连续的。 当然,这并不排除使用正弦和余弦特征来近似区间 \([0,\tau/2]\),这在某些情况下可能是有利的。
遵循这个逻辑并让 \(\tau=2\) 使得特征在半 \(\tau\) 区间 \([0,1]\) 上定义, 一维阶n傅里叶余弦基由 \(n+1\) 个特征组成
对 \(i=0, \dots, n\)。图9.3显示了一维傅立叶余弦特征 math:x_{i}, i=1,2,3,4, \(x_0\) 是常数函数。
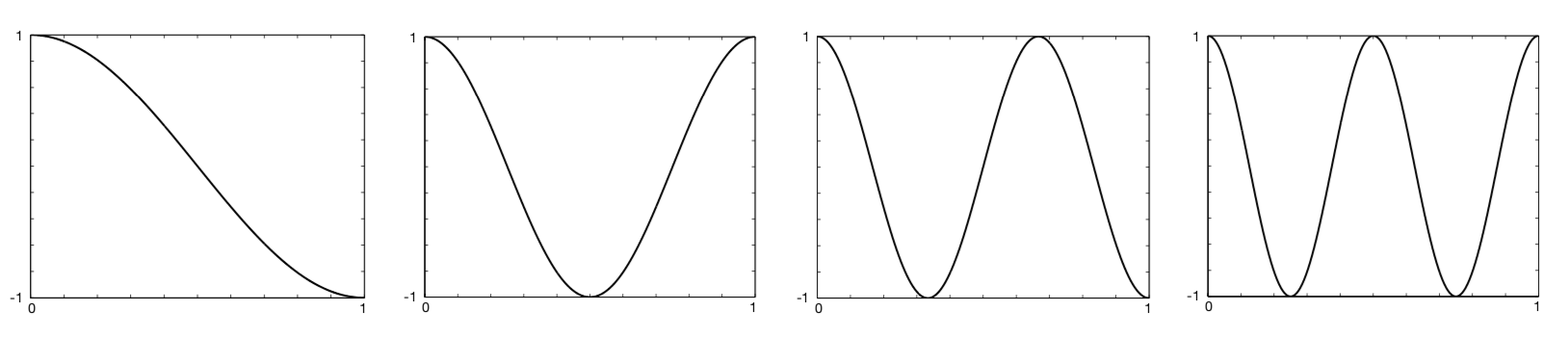
图9.3: 一维傅里叶余弦基特征 math:x_{i}, i=1,2,3,4,用于近似区间 \([0,1]\) 上的函数。 在Konidaris等人之后(2011年)。
同样的推理适用于下面方框中描述的多维情况下的傅立叶余弦序列近似。
注解
假设每个状态 \(s\) 对应于 \(k\) 个数的矢量, \(\mathbf{s}=(s_{1},s_{2},\ldots,s_{k})^{\top}\),每个 \(s_{i}\in[0,1]\)。 然后可以写出阶n傅里叶余弦基的第 \(i\) 个特征
其中 \(\mathbf{c}^{i}=(c_{1}^{i}, \ldots, c_{k}^{i})^{\top}\), 其中对 \(j=1, \dots, k\) 和 \(i=1, \dots,(n+1)^{k}\),\(c_{j}^{i} \in\{0, \dots, n\}\) 。 这为 \((n+1)^{k}\) 个可能的整数向量 \(\mathbf{c}^{i}\) 中的每一个定义了一个特征。 内积 \(\mathbf{s}^{\top} \mathbf{c}^{i}\) 具有在 \(\{0, \dots, n\}\) 中 分配整数到 \(\mathbf{s}\) 的每个维度的效果。 与在一维情况下一样,此整数确定沿该维度的特征频率。 当然,可以移动和缩放特征以适应特定应用的有界状态空间。
作为示例,考虑 \(k=2\) 的情况,其中 \(\mathbf{s}=(s_{1}, s_{2})^{\top}\), 其中每个 \(\mathbf{c}^{i}=(c_{1}^{i}, c_{2}^{i})^{\top}\)。 图9.4显示了六个傅里叶余弦特征的选择,每个特征由定义它的向量 \(\mathbf{c}^{i}\) 标记 (\(s_1\) 是水平轴,\(\mathbf{c}^{i}\) 显示为省略索引 \(i\) 的行向量)。 \(\mathbf{c}\) 中的任何零表示该特征沿该状态维度是恒定的。 因此,如果 \(\mathbf{c}=(0,0)^{\top}\),则该特征在两个维度上都是恒定的; 如果 \(\mathbf{c}=(c_{1}, 0)^{\top}\),特征在第二维上是恒定的,并且随着频率的变化而变化, 取决于 \(c_1\);并且对于 \(\mathbf{c}=(0, c_{2})^{\top}\) 也类似。 当 \(\mathbf{c}=(c_{1}, c_{2})^{\top}\) 且 \(c_{j}=0\) 时, 特征沿两个维度变化并表示两个状态变量之间的相互作用。 \(c_1\) 和 \(c_2\) 的值确定沿每个维度的频率,它们的比率给出了相互作用的方向。
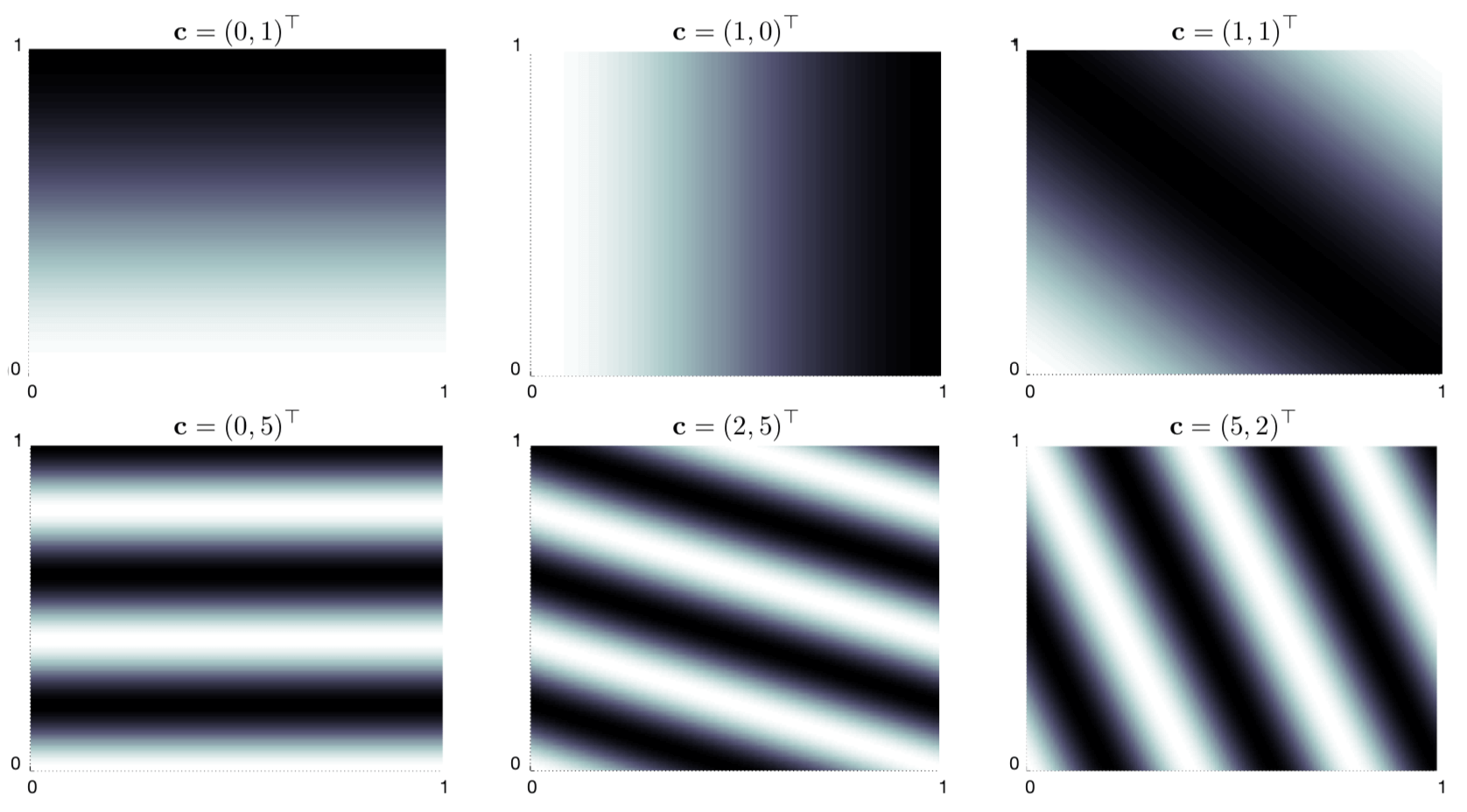
图9.4: 选择六个二维傅立叶余弦特征,每个特征由定义它的矢量 \(\mathbf{c}\) 标记 (\(s_1\) 是水平轴,\(\mathbf{c}^{i}\) 显示为省略索引 \(i\))。 在Konidaris等人之后(2011年)。
当使用傅立叶余弦特征和学习算法(如(9.7),半梯度TD(0)或半梯度Sarsa)时,为每个特征使用不同的步长参数可能会有所帮助。 如果 \(\alpha\) 是基本的步长参数,那么Konidaris,Osentoski和Thomas(2011)建议 将特征 \(x_i\) 的步长参数设置为 \(\alpha_i = \alpha / \sqrt{(c_{1}^{i})^{2}+\cdots+(c_{k}^{i})^{2}}\) (除非每个 \(c_j^i=0\),在这种情况下 \(\alpha_{i}=\alpha\))。
与其他几个基函数集合(包括多项式和径向基函数)相比,Sarsa的傅立叶余弦特征可以产生良好的性能。 然而,毫不奇怪,傅里叶特征在不连续性方面存在问题,因为除非包括非常高频率的基函数,否则很难避免在不连续点周围“转圈”。
阶n傅里叶基的特征数量随着状态空间的维数呈指数增长,但如果该尺寸足够小(例如,\(k \leq 5\)), 那么可以选择 \(n\) 以便所有的 \(n\) 阶傅立叶数特征可以使用。 这使得特征的选择或多或少是自动的。但是,对于高维状态空间,有必要选择这些特征的子集。 这可以使用关于要近似的函数的性质的先前信念来完成,并且可以调整一些自动选择方法以处理强化学习的增量和非平稳性质。 在这方面,傅里叶基本特征的优点在于,通过设置 \(\mathbf{c}^{i}\) 向量来解释状态变量之间可疑的相互作用, 并通过限制 \(\mathbf{c}^{i}\) 向量中的值以便近似可以滤除被认为是噪音的高频分量,可以很容易地选择特征。 另一方面,由于傅立叶特征在整个状态空间上都是非零的(除了少数零),它们代表状态的全局属性,这使得很难找到表示局部属性的好方法。
图9.5显示了在1000状态随机行走示例中比较傅立叶基和多项式的学习曲线。通常,我们不建议使用多项式进行在线学习 [2]。
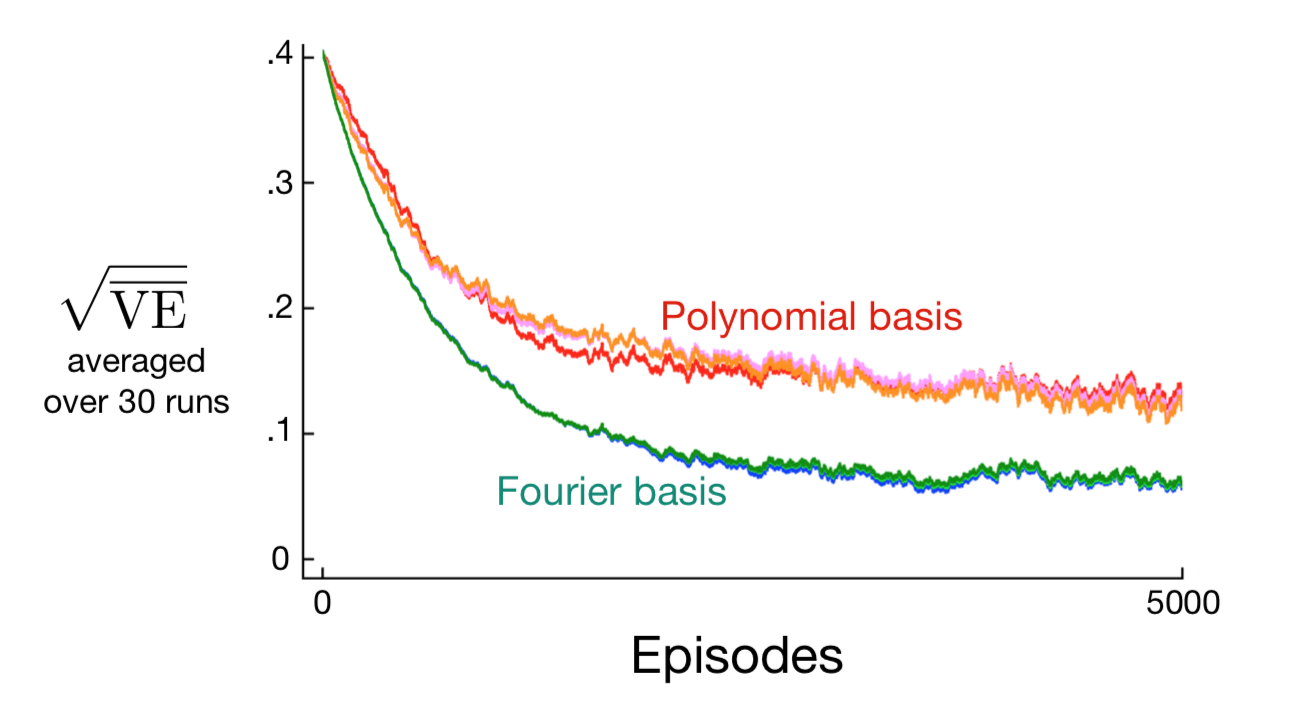
图9.5: 1000状态随机行走的傅立叶基与多项式对比。 展示了具有5,10和20阶傅立叶和多项式基的梯度蒙特卡罗方法的学习曲线。 对于每种情况粗略地优化步长参数:对于多项式,\(\alpha=0.0001\),对于傅立叶基,\(\alpha=0.00005\)。 性能度量(y轴)是均方根值误差(9.1)。
9.5.3 粗编码(Coarse Coding)¶
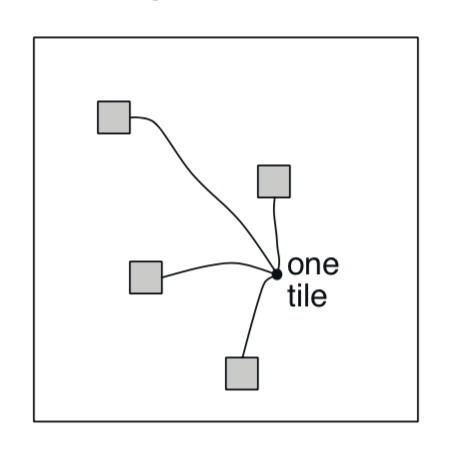
考虑一个任务,其中状态集的自然表示是连续的二维空间。这种情况的一种表示由与状态空间中的圆相对应的特征组成,如右侧所示。 如果状态在圆圈内,则相应的特征具有值1并且可以说是 存在(present);否则该特征为0并且可以说 不存在(absent)。 这种1-0值的特征称为 二元特征。给定状态,其二元特征存在指示状态位于圆内,并因此粗略地编码其位置。 表示具有以这种方式重叠的特征的状态(尽管它们不必是圆形或二元)被称为 粗编码。
假设线性梯度下降函数近似,考虑圆的大小和密度的影响。对应于每个圆圈是受学习影响的单个重量(\(\mathbf{w}\) 的分量)。 如果我们在一个状态,即空间中的一个点进行训练,那么与该状态相交的所有圆的权重都将受到影响。 因此,通过(9.8),近似价值函数将在圆的并集内的所有状态中受到影响,一个点与状态“共同”的圆圈越多,效果越大,如图9.6所示。 如果圆是小的,则泛化将在短距离上,如图9.7(左),而如果它们很大,它将在很大的距离上,如图9.7(中间)。 而且,特征的形状将决定泛化的性质。例如,如果它们不是严格的圆形,而是在一个方向上伸长,则可以类似地进行泛化,如图9.7(右)所示。
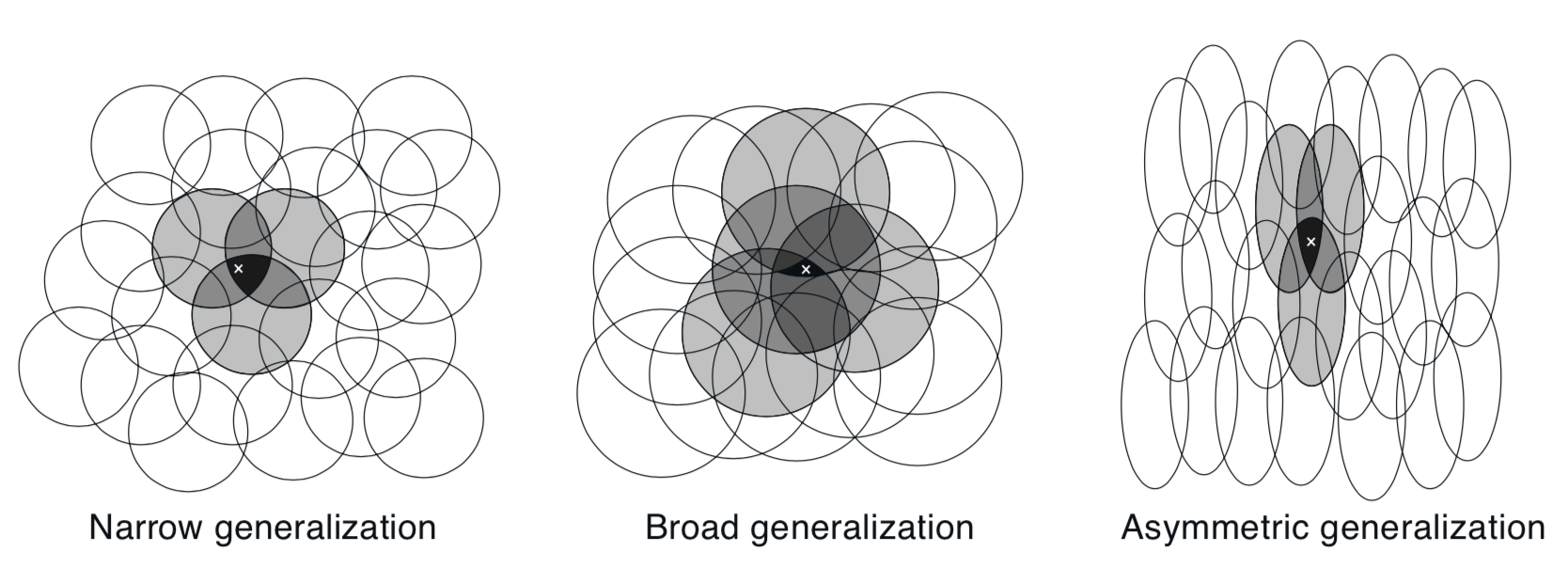
图9.7: 线性函数近似方法的泛化由特征的感受域的大小和形状决定。所有这三种情况的特征数量和密度大致相同。
具有大的感受域的特征给出了广泛的泛化,但似乎也可能将学习的函数限制为粗略的近似,不能使区分比感受域的宽度更精细。 令人高兴的是,事实并非如此。 从一个点到另一个点的初步泛化确实受到感受域的大小和形状的控制, 但最终可能的最佳辨别力的敏锐性更多地受到特征总数的控制。
例9.3:粗编码的粗糙度 这个例子说明了粗编码中学习感受域大小的影响。 基于粗编码的线性函数近似和(9.7)用于学习一维方波函数(如图9.8顶部所示)。 该函数的值用作目标 \(U_t\)。只有一个维度,感受域是间隔而不是圆圈。 重复学习有三种不同大小的间隔:窄,中和宽,如图的底部所示。 所有三个案例都具有相同的特征密度,在所学习的函数范围内约为50。在此范围内随机均匀地生成训练样例。 步长参数是 \(\alpha=\frac{0.2}{n}\),其中 \(n\) 是一次出现的特征数。 图9.8显示了在整个学习过程中在所有三种情况下学到的函数。请注意,特征的宽度在学习的早期具有很强的影响力。 具有广泛的特征,泛化趋于广泛;具有狭窄特征,只有每个训练点的邻近被改变,导致学习的函数更加颠簸。 但是,学习的最终函数仅受到特征宽度的轻微影响。感受域形状往往对泛化有很强的影响,但对渐近解的质量影响不大。
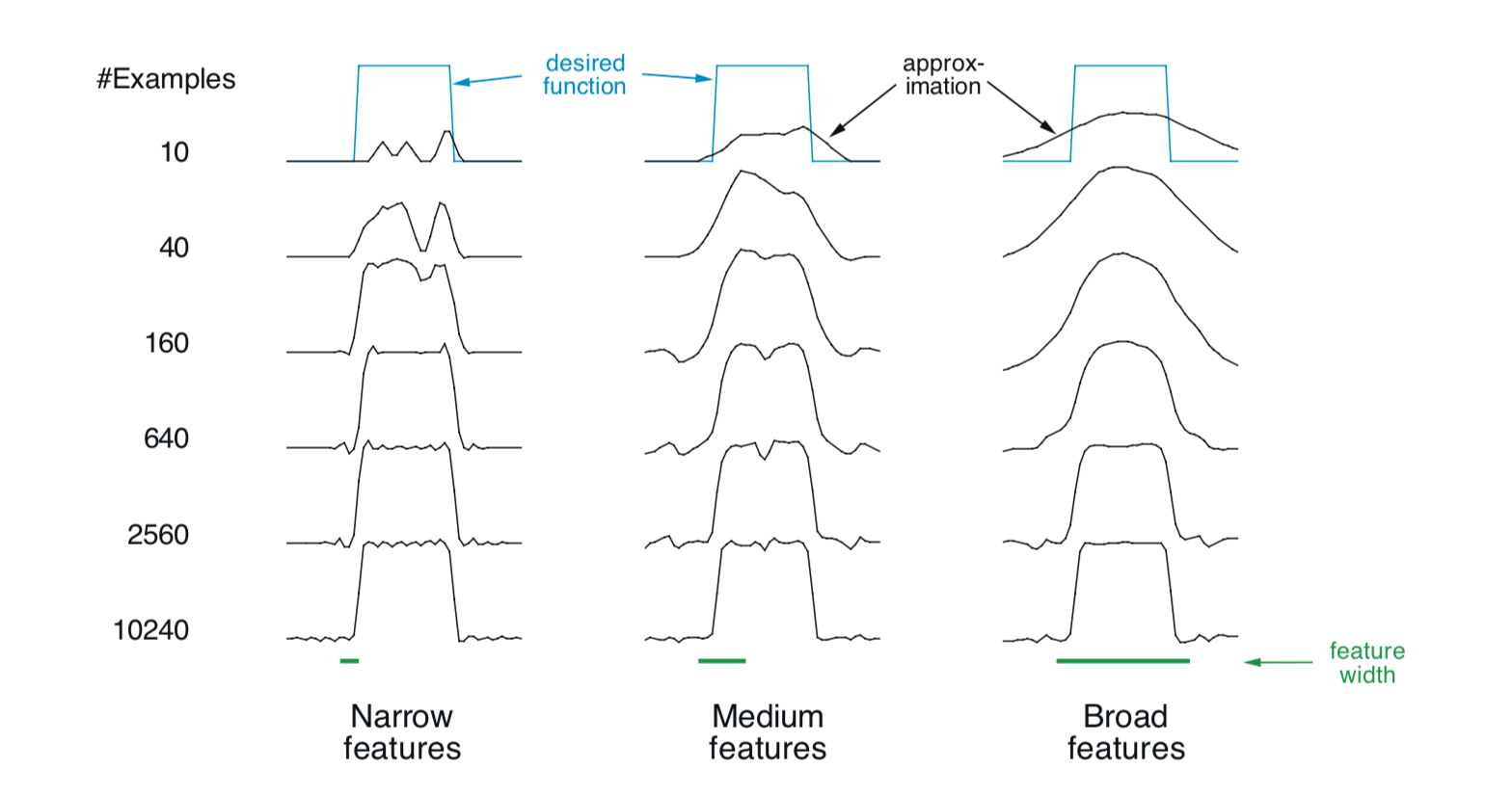
图9.8: 特征宽度对初始泛化(第一行)的强烈影响和对渐近精度(最后一行)的弱影响的示例。
9.5.4 铺片编码(Tile Coding)¶
平铺编码是多维连续空间的粗编码形式,其灵活且计算效率高。它可能是现代顺序数字计算机最实用的特征表示。
在平铺编码中,特征的感受域被分组为状态空间的分区。每个这样的分区称为 平铺(tiling),分区的每个元素称为 铺片(tile)。 例如,二维状态空间的最简单平铺是均匀网格,如图9.9左侧所示。这里的铺片或感受野是方形,而不是图9.6中的圆圈。 如果仅使用这个单一的平铺,那么白点所指示的状态将由其所在的单个特征表示;泛化将完成同一个铺片内的所有状态,并且不存在于其外的状态。 只有一个平铺,我们不会有粗编码,只是一个状态聚合的情况。
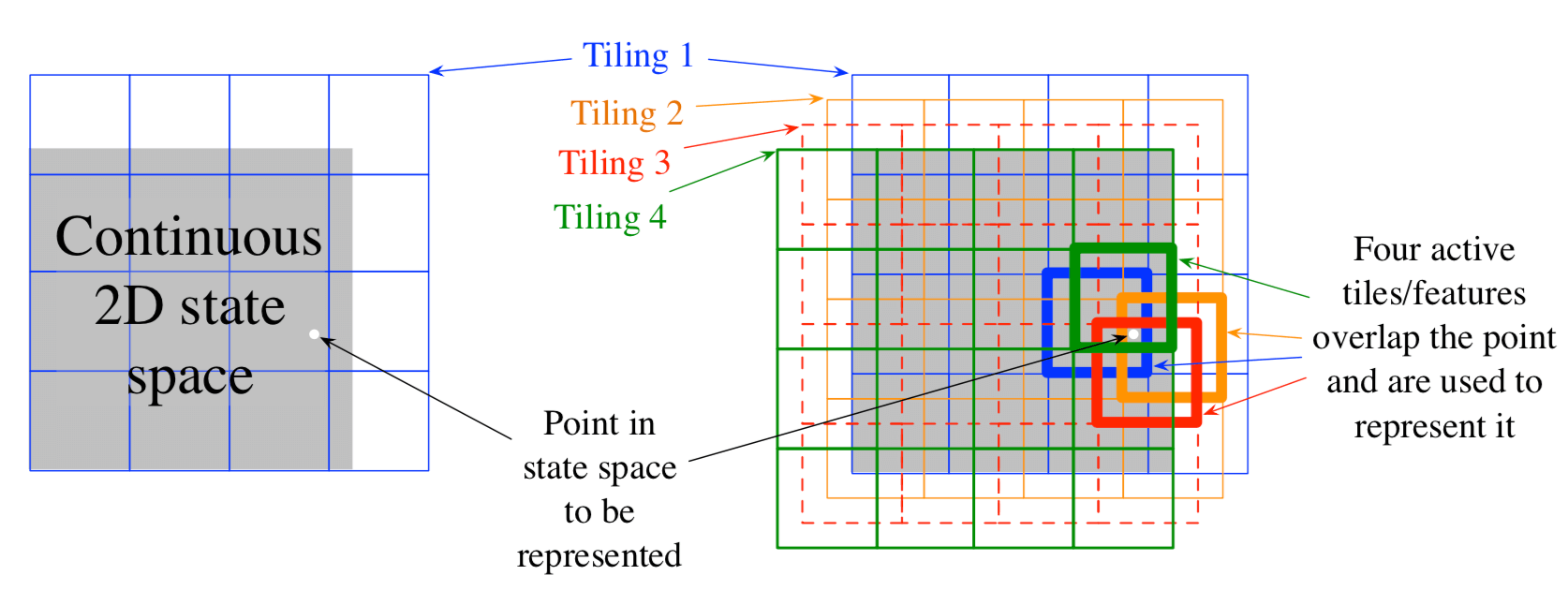
图9.9: 在有限的二维空间上的多个重叠网格平铺。这些平铺在每个维度上彼此偏移均匀的量。
为了获得粗编码的优势,需要重叠的感受域,并且根据定义,分区的铺片不重叠。 为了使用铺片编码获得真正的粗编码,使用多个平铺,每个平铺由铺片宽度的一小部分组成。 图9.9右侧显示了一个带有四个倾斜的简单箱子。每个状态,例如由白点指示的状态,在四个铺片中的每一个中恰好落入一个铺片中。 这四个图块对应于在状态发生时变为活动的四个特征。 具体地,特征向量 \(\mathbf{x}(s)\) 对于每个平铺中的每个铺片具有一个分量。 在这个例子中有 \(4 \times 4 \times 4 = 64\) 个分量, 除了与 \(s\) 落入的铺片相对应的四个分量外,所有分量都是0。 图9.10显示了1000状态随机行走示例中多个偏移平铺(粗编码)相较于单个平铺的优点。
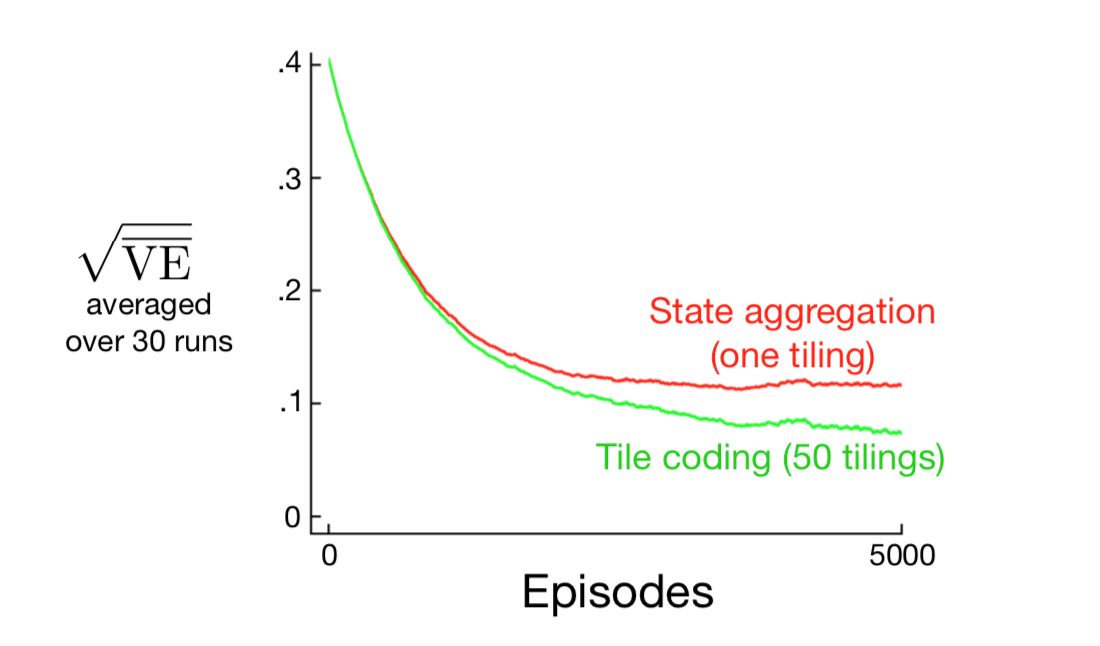
图9.10: 为什么我们使用粗编码。所示为1000状态随机行走示例的学习曲线,用于具有单个平铺和多个平铺的梯度蒙特卡罗算法。 1000个状态的空间被视为单个连续维度,覆盖有每200个状态宽的铺片。多个铺片相互偏移4个状态。 设置步长参数,使得两种情况下的初始学习率相同,单个平铺为 \(\alpha=0.0001\),50个铺片为 \(\alpha=0.0001/50\)。
铺片编码的直接实际优点在于,因为它适用于分区,所以一次激活的特征的总数对于任何状态都是相同的。 每个平铺中都存在一个特征,因此存在的特征总数始终与平铺数相同。这允许以简单,直观的方式设置步长参数 \(\alpha\)。 例如,选择 \(\alpha=\frac{1}{n}\),其中 \(n\) 是平铺的数量,从而产生精确的一次尝试(one-trial)学习。 如果是示例 \(s \mapsto v\) 训练,然后 无论先前的估计 \(\hat{v}(s, \mathbf{w}_t)\) 是多少, 新的估计将是 \(\hat{v}(s, \mathbf{w}_{t+1})=v\)。 通常人们希望改变比这更慢,以允许目标输出的泛化和随机变化。 例如,可以选择 \(\alpha=\frac{1}{10n}\),在这种情况下,训练状态的估计值将在一次更新中移动到目标的十分之一, 并且邻近状态将移动得更少,与它们共同的铺片数量成比例。
通过使用二元特征向量,铺片编码也获得了计算优势。因为每个分量都是0或1,所以构成近似价值函数(9.8)的加权和几乎是微不足道的。 与其执行 \(d\) 维乘法和加法,只需简单地计算 \(n \ll d\) 个活动特征的分片(indices), 然后将权重向量的 \(n\) 个相应分量相加。
如果这些状态落入任何相同的铺片内,则会对除训练的状态以外的状态进行泛化,与共同的铺片数成比例。 即使选择如何相互设置平铺也影响泛化。如果它们在每个维度上均匀分布,如图9.9所示,那么不同的状态可以以不同的方式泛化,如图9.11的上半部分所示。 八个子图中的每一个都显示了从训练状态到附近点的泛化模式。 在这个例子中,有八个平铺,因此一个铺片内的64个子区域明显地泛化,但都根据这八个模式之一。 请注意,在许多模式中,均匀偏移如何沿对角线产生强烈的效果。 如果平铺是不对称的,则可以避免这些伪影(artifacts),如图的下半部分所示。 这些较低的泛化模式更好,因为它们都很好地集中在训练状态,没有明显的不对称性。
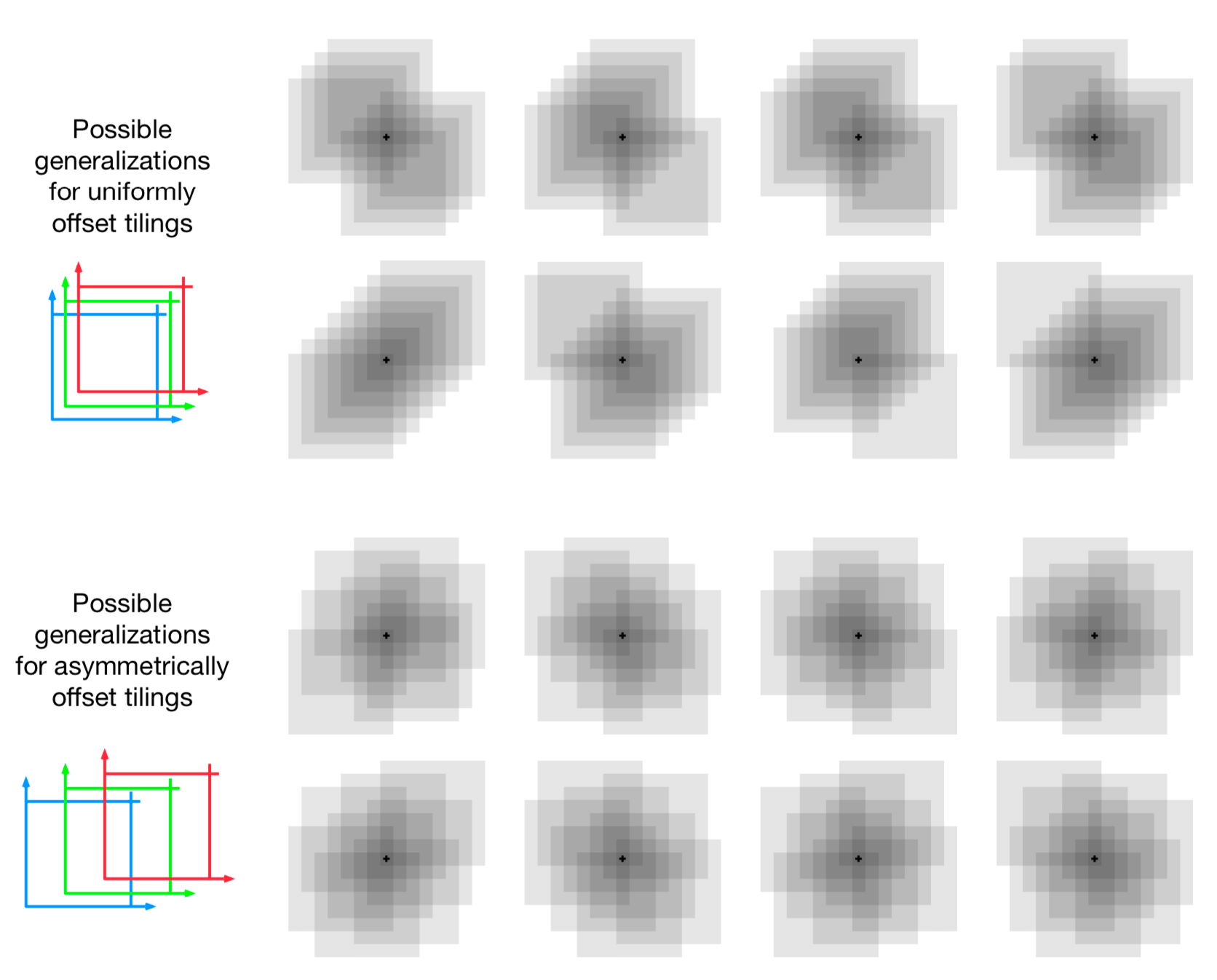
图9.11: 为什么在铺片编码中优选铺片非对称偏移。所显示的是从训练状态(由小黑加号表示)到附近状态的泛化的强度,对八个平铺的情况。 如果平铺均匀地偏移(上方),那么在对于泛化而言存在对角伪影和实质变化,而对于非对称偏移平铺,泛化更加球形和均匀。
在所有情况下,平铺在每个尺寸中相互偏移铺片宽度的一小部分。 如果 \(w\) 表示铺片宽度并且 \(n\) 表示平铺的数量,则 \(\frac{w}{n}\) 是基本单位。 在一侧的小方块 \(\frac{w}{n}\) 内,所有状态都激活相同的铺片,具有相同的特征表示和相同的近似值。 如果状态在任何笛卡尔方向上被移动 \(\frac{w}{n}\),则特征表示将更改一个分量/铺片。 均匀偏移平铺恰好相互偏移该单位距离。对于二维空间,我们说每个平铺都被位移矢量 \((1,1)\) 偏移, 这意味着它与之前的平铺偏移了 \(\frac{w}{n}\) 乘以此向量。在这些术语中, 图9.11下部所示的非对称偏移平铺偏移了 \((1,3)\) 的位移矢量。
对不同位移矢量对铺片编码泛化的影响进行了广泛的研究 (Parks和Militzer,1991;An,1991;An,Miller和Parks,1991;Miller,An,Glanz和Carter,1990), 评估它们对于对角伪影的本质和倾向,如 \((1,1)\) 位移矢量所见。 基于这项工作,Miller和Glanz(1996)建议使用由第一个奇数整数组成的位移矢量。 特别是,对于维数 \(k\) 的连续空间,一个很好的选择是使用第一个奇数整数(\(1,3,5,7, \ldots, 2 k-1\)), 其中 \(n\) (平铺数)设置为大于或等于 \(4k\) 的2的整数幂。 这就是我们在图9.11的下半部分中产生平铺所做的工作, 其中 \(k=2\),\(n=2^3 \ge 4k\),位移矢量是 \((1,3)\)。 在三维情况下,前四个平铺将从基准位置总计偏移 \((0,0,0)\),\((1,3,5)\),\((2,6,10)\) 和 \((3,9,15)\)。 开源软件可以很容易地为任何 \(k\) 做出像这样的平铺。
在选择平铺策略时,必须选择平铺的数量和平铺的形状。 平铺的数量以及铺片的大小决定了渐近近似的分辨率或精度,如通常的粗编码和图9.8所示。 铺片的形状将决定泛化的性质,如图9.7所示。方形铺片将在每个维度中大致相等,如图9.11(下图)所示。 沿一维延伸的铺片,如图9.12(中间)中的条纹倾斜,将促进沿该维度的泛化。 图9.12(中间)中的铺片在左侧也更密集和更薄,从而沿着该维度在较低值处促进沿水平维度的区分(discrimination)。 图9.12(右)中的平铺纹拼接将促进沿一个对角线的泛化。 在更高的维度中,轴对齐的条纹对应于忽略一些平铺中的一些尺寸,即,对于超平面切片。 如图9.12(左)所示的不规则平铺也是可能的,尽管在实践中很少见,并且超出了标准软件的能力范围。
图9.12: 平铺不必是网格。它们可以是任意形状和非均匀的,但在许多情况下仍然具有计算上的计算效率。
在实践中,通常希望在不同的平铺中使用不同形状的铺片。例如,可以使用一些垂直条纹平铺和一些水平条纹平铺。 这将鼓励沿任何一个方面进行泛化。然而,仅使用条纹平铺,不可能学到水平坐标和垂直坐标的特定连接具有独特的值 (无论学到什么,它将流入具有相同水平和垂直坐标的状态)。为此,需要连续的矩形瓷砖,如图9.9所示。 有多个平铺──一些是水平的,一些是垂直的,一些是连接的──我们可以得到一切: 偏好沿着每个维度进行泛化,但是能够学习连接的特定值(参见Sutton,1996的例子)。 平铺的选择决定了泛化,并且在这种选择可以有效地自动化之前,重要的是,铺片编码使得能够以对人们有意义的方式灵活地进行选择。
减少内存需求的另一个有用技巧是 散列(hashing) ──将大型平铺的一致伪随机分解成更小的铺片集。 散列产生的铺片由随机分布在整个状态空间中的不连续的不相交区域组成,但仍然形成一个全面的分区。 例如,一个铺片可能包含右侧所示的四个子铺片。通过散列,内存需求通常会被减低很大因子而几乎不会降低性能。 这是可能的,因为仅在状态空间的一小部分中需要高分辨率。 散列将我们从维度的诅咒中解放出来,因为内存需求不需要在维度数量上呈指数级别,而只需要匹配任务的实际需求。 铺片编码的开源实现通常包括高效散列。
练习9.4 假设我们认为两个状态维度中的一个更可能对价值函数产生影响而不是另一个维度,那么泛化应该主要跨越这个维度而不是沿着它。 可以使用什么样的平铺来利用这种先验知识?
9.5.5 径向基函数¶
径向基函数(RBF)是粗编码到连续值特征的自然泛化。 相较于每个特征都是0或1,它可以是区间 \([0,1]\) 中的任何值,反映特征所存在的不同 程度。 典型的RBF特征 \(x_i\) 具有高斯(钟形)响应 \(x_i(s)\), 其仅取决于状态 \(s\) 与特征的原型或中心状态 \(c_i\) 之间的距离,以及相对于特征的宽度 \(\sigma_i\):
当然,范数或距离度量可以以最适合于手头的状态和任务的任何方式来选择。下图显示了具有欧几里德距离度量的一维示例。
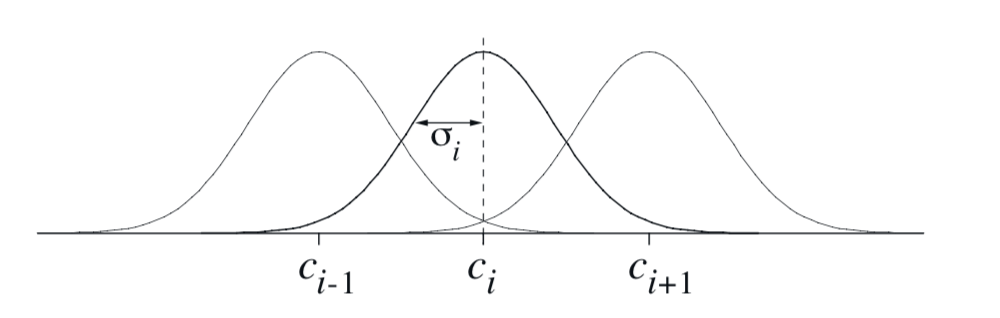
图9.13: 一维径向基函数
RBF相对于二元特征的主要优点是它们产生的近似函数平滑变化且可微。虽然这很吸引人,但在大多数情况下它没有实际意义。 然而,在铺片编码的背景下已经对分级响应函数(例如RBF)进行了广泛的研究 (An,1991;Miller等,1991;An等,1991;Lane,Handelman和Gelfand,1992)。 所有这些方法都需要相当大的额外计算复杂度(通过铺片编码),并且当存在多于两个状态维度时通常会降低性能。 在高维度中,铺片的边缘更加重要,并且已经证明难以在边缘附近获得良好控制的分级铺片激活。
RBF网络 是使用RBF作为其特征的线性函数近似器。等式(9.7)和(9.8)定义学习,与其他线性函数近似器完全相同。 此外,RBF网络的一些学习方法也改变了特征的中心和宽度,使它们进入非线性函数近似的领域。非线性方法可以更精确地拟合目标函数。 RBF网络,特别是非线性RBF网络的缺点是计算复杂度更高,并且通常在学习之前进行更多的手动调整是健壮且有效的。
9.6 手动选择步长参数¶
大多数SGD方法都要求设计者选择合适的步长参数 \(\alpha\)。 理想情况下,这种选择将是自动化的,并且在某些情况下一直是这样,但在大多数情况下,通常的做法是手动设置它。 要做到这一点,并且为了更好地理解算法,开发对步长参数作用的直觉是很有用的。我们可以说一般应该如何设置呢?
遗憾的是,理论上的考虑没什么帮助。随机近似理论给出了缓慢递减的步长序列的条件(2.7),这些序列足以保证收敛,但这些往往导致学习太慢。 在表格MC方法中产生样本平均值的经典选择 \(\alpha_t=1/t\) 不适用于TD方法,非平稳问题或任何使用函数近似的方法。 对于线性方法,存在设置最佳 矩阵 步长的递归最小二乘法,并且这些方法可以扩展到时序差分学习,如第9.8节中描述的LSTD方法, 但这些方法需要 \(O\left(d^{2}\right)\) 步长参数,或者比我们学习的参数多 \(d\) 倍。 出于这个原因,我们将它们排除在最需要函数近似的大型问题上。
为了直观地了解如何手动设置步长参数,最好立即回到表格例子。 在那里我们可以理解,步长为 \(\alpha=1\) 将导致在一个目标之后完全消除样本误差(参见(2.4)步长为1)。 正如第9.3节所讨论的,我们通常希望学习比这更慢。 在表格的情况下,步长为 \(\alpha=\frac{1}{10}\) 将需要大约10个经验到大致收敛到它们的平均目标, 如果我们想要在100个经验中学习,我们将使用 \(\alpha=\frac{1}{100}\)。 一般来说,如果 \(\alpha=\frac{1}{\tau}\), 那么一个状态的表格估计在关于状态的 \(\tau\) 次经验后将接近其目标的均值,最近的目标效果最好。
对于一般函数近似,没有关于状态的经验 数量 的这种明确概念,因为每个状态可能与所有其他状态在不同程度上相似和不相似。 然而,在线性函数近似的情况下,存在类似的规则。假设你想在 \(\tau\) 个经验内用大致相同的特征向量来学习。 然后,设置线性SGD方法的步长参数的一个好的经验法则是
其中,\(\mathbf{x}\) 是从与SGD中的输入矢量相同的分布中选择的随机特征向量。 如果特征向量的长度变化不大,则此方法效果最佳;理想情况下,\(\mathbf{x}^{\top} \mathbf{x}\) 是常数。
练习9.5 假设你正在使用铺片编码将七维连续状态空间转换为二元特征向量, 以估计状态价值函数 \(\hat{v}(s,\mathbf{w})\approx v_\pi(s)\)。 你认为维度不会强烈相互作用,因此你决定分别使用每个维度的八个平铺(条纹平铺),共 \(7 \times 8=56\) 个平铺。 此外,如果维度之间存在一些成对的相互作用, 你还可以采用所有 \(\left(\begin{array}{l}{7}\\{2}\end{array}\right)=21\) 对维度,并将每对维度与矩形铺片相连。 你为每对维度进行两次平铺,总计 \(21 \times 2 + 56 = 98\) 个平铺。 对于这些特征向量,你怀疑你仍然需要平均一些噪音,因此你决定要学习循序渐进,在学习接近渐近线之前,用相同的特征向量进行大约10次展示。 你应该使用什么步长参数?为什么?
9.7 非线性函数近似:人工神经网络¶
人工神经网络(ANN)广泛用于非线性函数近似。ANN是一个互联单元的网络,具有神经元的某些特性,神经元是神经系统的主要组成部分。 人工神经网络历史悠久,最新的深层人工神经网络(深度学习)训练是机器学习系统中最令人印象深刻的能力,包括强化学习系统。 在第16章中,我们描述了使用ANN函数近似的强化学习系统的几个令人印象深刻的例子。
图9.14显示了一个通用的前馈ANN,意味着网络中没有环路,也就是说,网络中没有路径可以通过单元的输出影响其输入。 图中的网络具有由两个输出单元组成的输出层,具有四个输入单元的输入层和两个“隐藏层”:既不是输入层也不是输出层的层。 实值权重与每个链接相关联。权重大致对应于真实神经网络中突触连接的流动性(参见第15.1节)。 如果ANN在其连接中至少有一个循环,则它是一个循环而不是前馈ANN。 虽然前馈和循环人工神经网络都已用于强化学习,但在这里我们只考虑更简单的前馈情况。
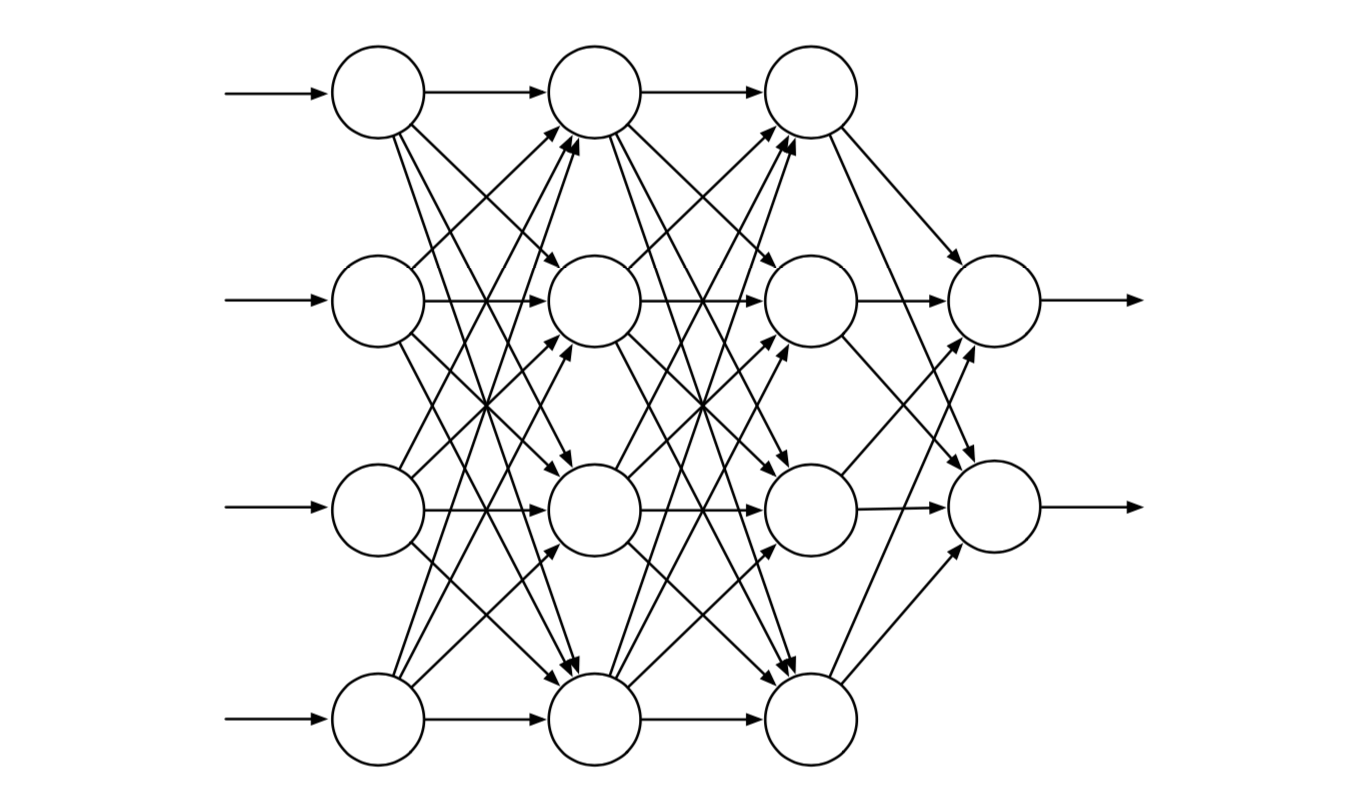
图9.14: 具有四个输入单元,两个输出单元和两个隐藏层的通用前馈ANN。
单元(图9.14中的圆圈)通常是半线性单单元,这意味着它们计算输入信号的加权和, 然后将非线性函数(称为 激活函数)应用于结果,以生成单元的输出或激活。 使用了不同的激活函数,但它们通常是S形或sigmoid,例如逻辑函数 \(f(x)=1 /\left(1+e^{-x}\right)\), 尽管有时使用整流非线性 \(f(x)=\max (0, x)\)。 如果 \(x\geq\theta\),则阶梯函数如 \(f(x)=1\),否则为0,得到具有阈值 \(\theta\) 的二进制单元。 网络输入层中的单元在将其激活设置为外部提供的值时有些不同,这些值是网络近似的函数的输入。
前馈ANN的每个输出单元的激活是网络输入单元上的激活模式的非线性函数。这些函数由网络的连接权重参数化。 没有隐藏层的ANN只能代表可能的输入输出函数的一小部分。 然而,具有单个隐藏层的ANN包含足够大的有限数量的S形单元,可以在网络输入空间的紧凑区域上近似任何连续函数, 达到任何精确度(Cybenko,1989)。对于满足温和条件的其他非线性激活函数也是如此,但非线性是必不可少的: 如果多层前馈ANN中的所有单元都具有线性激活函数,则整个网络相当于没有隐藏层的网络(因为线性函数的线性函数本身是线性的)。
尽管单隐藏层人工神经网络具有这种“通用近似”特性,但经验和理论都表明, 近似许多人工智能任务所需的复杂函数变得更加容易──实际上可能需要抽象,这些抽象是多层低级的分层组合, 即由具有许多隐藏层的人工神经网络等深层架构产生的抽象。(参见Bengio,2009,进行彻底的复习。) 深层ANN的连续层计算网络“原始”输入的逐渐抽象表示,每个单元提供有助于网络的整体输入-输出功能的分层表示的特征。
因此,训练ANN的隐藏层是一种自动创建适合于给定问题的特征的方法,从而可以在不依赖于手工选择的特征的情况下生成分层表示。 这对人工智能来说一直是一个持久的挑战,并解释了为什么具有隐藏层的人工神经网络的学习算法多年来受到如此多的关注。 人工神经网络通常通过随机梯度法学习(第9.3节)。每个权重的调整方向旨在改善网络的整体性能,如通过目标函数测量的最小化或最大化。 在最常见的监督学习案例中,目标函数是一组标记的训练样例的预期误差或损失。 在强化学习中,人工神经网络可以使用TD误差来学习价值函数,或者他们的目标是最大化预期奖励,如梯度老虎机(第2.8节)或策略梯度算法(第13章)。 在所有这些情况下,有必要估计每个连接权重的变化将如何影响网络的整体性能,换句话说,估计目标函数相对于每个权重的偏导数,给定网络权重的所有当前值。 梯度是这些偏导数的矢量。
对于具有隐藏层的人工神经网络(如果单元具有不可激活的激活函数),最成功的方法是反向传播算法,它包括通过网络的交替前向和后向传递。 在给定网络输入单元的当前激活的情况下,每个前向传递计算每个单元的激活。在每次前进之后,后向传递有效地计算每个权重的偏导数。 (与其他随机梯度学习算法一样,这些偏导数的向量是对真实梯度的估计。) 在15.10节中,我们讨论了使用强化学习原理而不是反向传播来训练具有隐藏层的ANN的方法。 这些方法不如反向传播算法有效,但它们可是能更接近真实神经网络的学习方式。
反向传播算法可以为具有1或2个隐藏层的浅网络产生良好的结果,但是对于更深的ANN可能不能很好地工作。 实际上,训练具有 \(k+1\) 个隐藏层的网络实际上可能导致比使用 \(k\) 个隐藏层的网络训练更差的性能, 即使更深的网络可以代表更浅网络的所有功能(Bengio,2009)。解释这些结果并不容易,但有几个因素很重要。 首先,典型深度ANN中的大量权重使得难以避免过度拟合的问题,即,未能正确地泛化到网络未训练过的情况的问题。 其次,反向传播对于深度神经网络效果不佳,因为其向后传递计算的偏导数 要么快速衰减到网络的输入端,使得深层学习极慢,要么偏导数快速向输入侧增长,使学习不稳定。 处理这些问题的方法是使用深度神经网络的系统所取得的许多令人印象深刻的最新结果的主要原因。
过拟合是任何函数近似方法的问题,该方法基于有限的训练数据调整具有多个自由度的函数。 对于不依赖有限训练集的在线强化学习而言,这不是一个问题,但有效泛化仍然是一个重要问题。 过拟合一般是人工神经网络的问题,但对于深度人工神经网络尤其如此,因为它们往往具有非常大的权重。 已经开发了许多方法来减少过度拟合。这些包括在不同于训练数据(交叉验证)的验证数据上性能开始下降时停止训练, 修改目标函数以阻止近似的复杂性(正则化),以及引入权重之间的依赖性以减少自由度的数量(例如,权重分享)。
一种用于减少深度神经网络过度拟合的特别有效的方法是由Srivastava,Hinton,Krizhevsky,Sutskever和Salakhutdinov(2014)引入的dropout方法。 在训练期间,单元及其连接随机从网络中删除。这可以被认为是训练大量“稀疏”网络。在测试时结合这些稀疏网络的结果是提高泛化性能的一种方法。 dropout方法通过将单元的每个输出权重乘以训练期间保留该单元的概率来有效地近似该组合。 Srivastava等人发现这种方法显着提高了泛化性能。它鼓励个别隐藏单元学习与其他特征的随机集合配合良好的特征。 这增加了由隐藏单元形成的特征的多功能性,使得网络不会过度专注于很少发生的情况。
Hinton,Osindero和Teh(2006)在深度信念网络,与这里讨论的深层人工神经网络密切相关的分层网络中, 在解决深层人工神经网络深层训练问题上迈出了重要一步。在他们的方法中,使用无监督学习算法一次一个地训练最深层。 在不依赖于整体目标函数的情况下,无监督学习可以提取捕获输入流的统计规律的特征。 首先训练最深层,然后通过该训练层提供输入,训练下一个最深层,依此类推,直到网络层中所有或多个层中的权重设置为现在作为初始的值用于监督学习。 然后通过关于整体目标函数的反向传播来微调网络。研究表明,这种方法通常比使用随机值初始化的权重的反向传播更好。 以这种方式初始化的权重训练的网络的更好性能可能是由于许多因素造成的, 但是一种想法是该方法将网络置于权重空间区域中,基于梯度的算法可以从中获得良好的进展。
批量标准化 (Ioffe和Szegedy,2015)是另一种可以更容易地训练深度人工神经网络的技术。 人们早就知道,如果网络输入被标准化,则ANN学习更容易,例如,通过将每个输入变量调整为具有零均值和单位方差。 用于训练深度ANN的批量标准化将深层的输出在进入下一层之前进行标准化。 Ioffe和Szegedy(2015)使用来自训练样例的子集或“小批量”的统计来归一化这些层间信号,以提高深度ANN的学习率。
另一种用于训练深度ANN的技术是 深度残差学习 (He,Zhang,Ren和Sun,2016)。有时,学习函数与恒等函数的区别比学习函数本身更容易。 然后将该差值,即残差函数添加到输入产生所需的函数。 在深度人工神经网络中,只需在块周围添加快捷方式或跳过连接,就可以制作一个层块来学习残差函数。 这些连接将块的输入添加到其输出,并且不需要额外的权重。He等人(2016)使用深度卷积网络评估该方法, 该网络具有围绕每对相邻层的跳过连接,在没有基准图像分类任务上的跳过连接的情况下发现对网络的实质性改进。 批量标准化和深度残差学习都用于我们在第16章中描述的围棋游戏的强化学习应用程序。
已经证明在应用中非常成功的一种深度ANN,包括令人印象深刻的强化学习应用(第16章),是 深度卷积网络。 这种类型的网络专门用于处理以空间阵列(例如图像)排列的高维数据。 它的灵感来自早期视觉处理在大脑中的运作方式(LeCun,Bottou,Bengio和Haffner,1998)。 由于其特殊的结构,深度卷积网络可以通过反向传播进行训练,而无需采用上述方法来训练深层。
图9.15说明了深度卷积网络的体系结构。这个例子来自LeCun等人(1998),旨在识别手写字符。 它由交替的卷积和子采样层组成,接着是几个完全连接的最终层。每个卷积层产生许多特征映射。 特征映射是对单元阵列的活动模式,其中每个单元对其感受域中的数据执行相同的操作, 该感受域是从前一层(或第一卷积层的情况下来自外部输入)中“看到”的数据的一部分。 特征映射的单元彼此相同,只是它们的感受域(大小和形状都相同)被移动到输入数据数组上的不同位置。 同一特征映射中的单元共享相同的权重。这意味着无论在输入数组中的哪个位置,特征映射都会检测到相同的特征。 例如,在图9.15的网络中,第一个卷积层产生6个特征映射,每个映射由 \(28 \times 28\) 个单元组成。 每个特征映射中的每个单元都有一个 \(5 \times 5\) 的感受域,这些感受域重叠(在这种情况下是四列四行)。 因此,6个特征映射中的每一个仅由25个可调整权重指定。
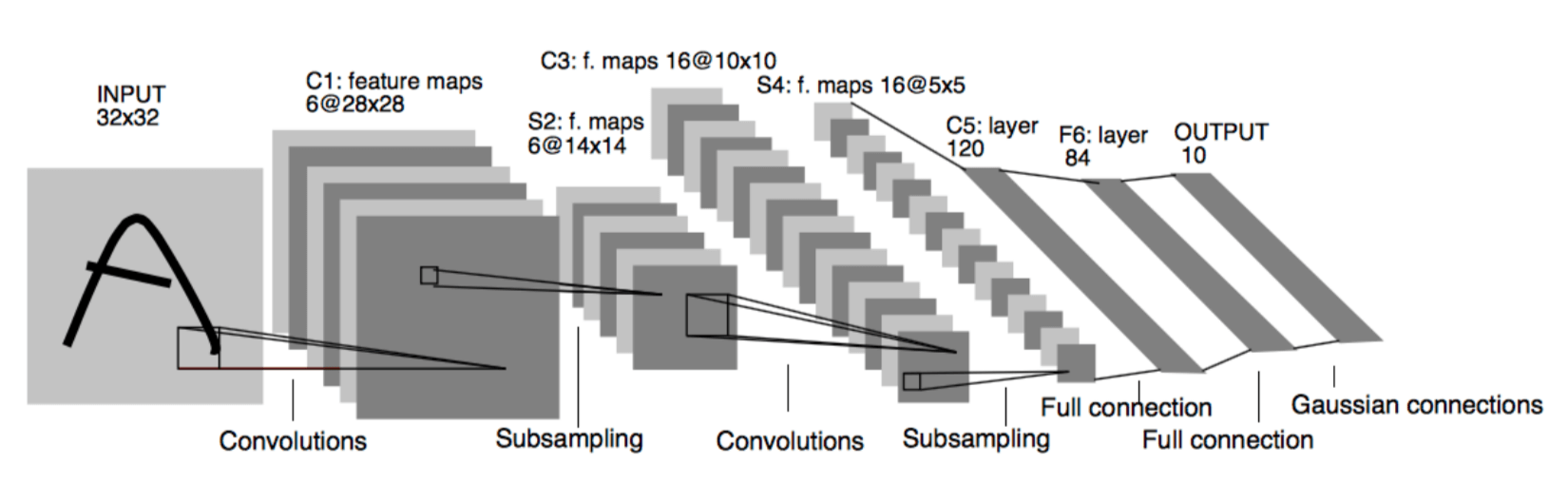
图9.15: 深度卷积网络。经过IEEE会议论文的许可,重新发布,从基于梯度的学习应用于文档识别, LeCun,Bottou,Bengio和Haffner,第86卷,1998年;通过Copyright Clearance Center, Inc传达许可。
深度卷积网络的子采样层降低了特征映射的空间分辨率。子采样层中的每个特征映射由在前一个卷积层的特征映射中的单元的感受域上平均的单元组成。 例如,图9.15的网络的第一个子采样层中的6个特征映射中的每一个中的每个单元 在由第一卷积层产生的特征映射之一上的 \(2 \times 2\) 非重叠感受域上平均,产生六个 \(14 \times 14\) 特征映射。 子采样层降低了网络对检测到的特征的空间位置的敏感度,也就是说,它们有助于使网络的响应在空间上不变。 这很有用,因为在图像中的某个位置检测到的特征也可能在其他地方有用。
人工神经网络的设计和训练的进展──我们只提到了一些,都有助于强化学习。 虽然目前的强化学习理论主要局限于使用表格或线性函数近似方法的方法, 但值得注意的强化学习应用的令人印象深刻的表现很大程度上归功于多层人工神经网络的非线性函数近似。 我们将在第16章讨论其中的几个应用程序。
9.8 最小二乘TD¶
到目前为止我们在本章中讨论过的所有方法都要求每个时步的计算与参数的数量成比例。 然而,通过更多计算,人们可以做得更好。在本节中,我们提出了一种线性函数近似的方法,可以说是这种情况下最好的方法。
正如我们在9.4节TD(0)中建立的线性函数近似渐近收敛(适当减小步长)到TD固定点:
其中
有人可能会问,为什么我们必须迭代地计算这个解决方案?这浪费了数据! 通过计算 \(\mathbf{A}\) 和 \(\mathbf{b}\) 的估计值,然后直接计算TD固定点,可能会做得更好吗? 最小二乘TD 算法,通常称为LSTD,就是这样做的。它形成了自然估计
其中 \(\mathbf{I}\) 是单位矩阵,对于一些小 \(\varepsilon>0\), \(\varepsilon\mathbf{I}\) 确保 \(\widehat{\mathbf{A}}_{t}\) 始终是可逆的。 似乎这些估计值都应该除以 \(t\),实际上它们应该是; 如这里定义的, 这些实际上是 \(t\) 乘 \(\mathbf{A}\) 和 \(t\) 乘 \(\mathbf{b}\) 的估计。 然而,当LSTD使用这些估计来估计TD固定点时,额外的 \(t\) 因子抵消了
该算法是线性TD(0)的最具数据效率的形式,但它在计算上也更昂贵。 回想一下,半梯度TD(0)需要仅仅 \(O(d)\) 的内存和每步计算。
LSTD有多复杂?如上所述,复杂性似乎随着 \(t\) 增加,但是(9.20)中的两个近似 可以使用我们之前介绍的技术(例如,在第2章中)逐步实现,以便它们每步可以在恒定时间内完成。 即便如此,\(\widehat{\mathbf{A}}_{t}\) 的更新将涉及外积(列向量乘以行向量),因此将是矩阵更新; 其计算复杂度为 \(O(d^2)\),当然保存 \(\widehat{\mathbf{A}}_{t}\) 矩阵 所需的内存为 \(O(d^2)\)。
一个潜在的更大问题是我们的最终计算(9.21)使用 \(\widehat{\mathbf{A}}_{t}\) 的逆, 并且一般逆计算的计算复杂度是 \(O(d^3)\)。 幸运的是,我们的特殊形式矩阵的逆矩阵──外积的总和,也可以仅通过 \(O(d^2)\) 计算逐步更新,即
对于 \(t>0\) 有 \(\widehat{\mathbf{A}}_{0}\doteq\varepsilon\mathbf{I}\)。 虽然称为 Sherman-Morrison公式 的恒等式(9.22)表面上很复杂, 但它只涉及矢量-矩阵和矢量-矢量乘法,因此只有 \(O(d^2)\)。 因此,我们可以存储逆矩阵 \(\widehat{\mathbf{A}}_{t}^{-1}\),用(9.22)计算它, 然后在(9.21)中使用它,所有都只有 \(O(d^2)\) 内存和每步计算。完整的算法在下面的框中给出。
LSTD估计 \(\hat{v}=\mathbf{w}^{\top} \mathbf{x}(\cdot) \approx v_{\pi}\) (\(O(d^2)\) 版本)
输入:特征表示 \(\mathbf{x} : \mathcal{S}^{+} \rightarrow \mathbb{R}^{d}\) 使得 \(\mathbf{x}(终止)=0\)
算法参数:小 \(\varepsilon>0\)
\(\widehat{\mathbf{A}^{-1}} \leftarrow \varepsilon^{-1} \mathbf{I}\),一个 \(d\times d\) 矩阵
\(\widehat{\mathbf{b}} \leftarrow \mathbf{0}\),一个 \(d\) 维度向量
对每一回合循环:
初始化 \(S\);\(\mathbf{x} \leftarrow \mathbf{x}(S)\)
对回合的每一步循环:
选择并采取动作 \(A \sim \pi(\cdot | S)\),观察 \(R, S^{\prime}\);\(\mathbf{x}^{\prime} \leftarrow \mathbf{x}(S^{\prime})\)
\(\mathbf{v} \leftarrow \widehat{\mathbf{A}^{-1}}^{\top} \left(\mathbf{x}-\gamma \mathbf{x}^{\prime}\right)\)
\(\widehat{\mathbf{A}^{-1}} \leftarrow \widehat{\mathbf{A}^{-1}}-\left(\widehat{\mathbf{A}^{-1}} \mathbf{x}\right) \mathbf{v}^{\top} /\left(1+\mathbf{v}^{\top} \mathbf{x}\right)\)
\(\widehat{\mathbf{b}} \leftarrow \widehat{\mathbf{b}}+R \mathbf{x}\)
\(\mathbf{w} \leftarrow \widehat{\mathbf{A}^{-1}} \widehat{\mathbf{b}}\)
\(S \leftarrow S^{\prime}\);\(\mathbf{x} \leftarrow \mathbf{x}^{\prime}\)
直到 \(S^{\prime}\) 终止
当然,\(O(d^2)\) 仍然比半梯度TD的 \(O(d)\) 消耗更多。 LSTD的更高数据效率是否值得计算花费取决于 \(d\) 的大小,快速学习的重要性以及系统其他部分的费用。 LSTD不需要步长参数的事实有时也被吹捧,但这可能被夸大了。LSTD不需要步长,但它确实需要 \(\varepsilon\); 如果 \(\varepsilon\) 选择得太小,逆的序列可能变化很大,如果 \(\varepsilon\) 选择得太大,那么学习速度会慢。 此外,LSTD缺乏步长参数意味着它永远不会忘记。这有时是可取的,但如果目标策略 \(\pi\) 在强化学习和GPI中发生变化则存在问题。 在控制应用中,LSTD通常必须与其他一些机制相结合,以引起遗忘,模糊不需要步长参数的任何初始优势。
9.9 基于内存的函数近似¶
到目前为止,我们已经讨论了近似价值函数的 参数 方法。 在该方法中,学习算法调整用于在问题的整个状态空间上近似价值函数的函数形式的参数。 每次更新 \(s \mapsto g\) 是学习算法用于改变参数的训练样例,目的是减少近似误差。 更新后,可以丢弃训练样例(尽管可以保存它以便再次使用)。当需要状态的近似价值(我们将称之为 查询状态)时, 使用学习算法产生的最新参数在该状态下简单地评估该函数。
基于内存的函数近似方法非常不同的。他们只需将训练样例保存在内存中(或者至少保存一部分样例)而不更新任何参数。 然后,每当需要查询状态的价值估计时,从内存检索一组样例并用于计算查询状态的价值估计。 这种方法有时被称为 延迟学习,因为处理训练样例被推迟,直到查询系统以提供输出。
基于内存的函数近似方法是 非参数 方法的主要示例。与参数方法不同,近似函数的形式不限于固定的参数化函数类, 例如线性函数或多项式,而是由训练样本本身确定,以及将它们组合到输出查询状态的估计值的一些方法。 随着越来越多的训练样例在内存中累积,人们希望非参数方法能够生成越来越准确的任何目标函数的近似值。
有许多不同的基于内存的方法,具体取决于如何选择存储的训练样例以及如何使用它们来响应查询。 在这里,我们关注 局部学习(local-learning) 方法,这些方法仅在当前查询状态的邻域中本地近似价值函数。 这些方法从内存中检索一组训练样例,其状态被判断为与查询状态最相关,其中相关性通常取决于状态之间的距离: 训练样例的状态越接近查询状态,它就被认为是越相关,其中距离可以以许多不同的方式定义。在给查询状态赋值之后,丢弃局部近似。
基于内存的方法的最简单示例是 最近邻(nearest neighbor) 方法, 其仅在内存中找到其状态最接近查询状态的样例,并将该样例的值作为查询状态的近似价值返回。 换句话说,如果查询状态是 \(s\),\(s^{\prime} \mapsto g\) 是内存中的样例, 其中 \(s^{\prime}\) 是与 \(s\) 最接近的状态,则 \(g\) 作为 \(s\) 的近似价值返回。 稍微复杂的是 加权平均 方法,其检索一组最近邻居样例并返回其目标值的加权平均值, 其中权重通常随着其状态与查询状态之间的距离增加而减小。 局部加权回归 是类似的,但它通过参数近似方法将表面拟合到一组最近状态的值, 该方法最小化加权误差测量,如(9.1),其中权重取决于与查询状态的距离。 返回的值是在查询状态下对局部拟合曲面的求值,之后丢弃局部近似曲面。
作为非参数的,基于内存的方法具有优于参数方法的优点,所述参数方法不限制对预先指定的函数形式的近似。 随着更多数据的累积,这可以提高准确性。基于内存的局部近似方法具有其他属性,使其非常适合强化学习。 由于轨迹采样在强化学习中非常重要,如第8.6节所述,基于内存的局部方法可以将函数近似集中在实际或模拟轨迹中访问的状态(或状态-动作对)的局部邻域上。 可能不需要全局近似,因为状态空间的许多区域将永远(或几乎从未)到达。 此外,与参数方法需要逐步调整全局近似的参数相比,基于内存的方法允许个体的经验对当前状态附近的价值估计具有相对直接的影响。
避免全局近似也是解决维度诅咒的一种方法。 例如,对于具有 \(k\) 维的状态空间,存储全局近似的表格方法需要内存为 \(k\) 的指数。 另一方面,在存储用于基于内存的方法的样例时,每个样例需要与 \(k\) 成比例的内存, 并且存储例如 \(n\) 个样例所需的内存关于 \(n\) 是线性的。\(k\) 或 \(n\) 中没有任何指数。 当然,关键的剩余问题是基于内存的方法是否能够足够快地回答查询以对个体有用。 一个相关的问题是随着内存大小的增长速度如何降低。在大型数据库中查找最近邻居可能需要很长时间才能在许多应用程序中实用。
基于内存的方法的支持者已经开发出加速最近邻搜索方法。 使用并行计算机或专用硬件是一种方法;另一种是使用特殊的多维数据结构来存储训练数据。 为该应用研究的一种数据结构是 \(k-d\) 树(\(k\) 维树的简称), 其递归地将 \(k\) 维空间分成组织为二叉树的节点的区域。 根据数据量及其在状态空间中的分布情况,使用 \(k-d\) 树的最近邻搜索可以在搜索邻居时快速消除空间的大区域, 使搜索在一些简单(naive)搜索也会花费长时间的问题上变得可行。
局部加权回归还需要快速方法来进行局部回归计算,必须重复这些回归计算以回答每个查询。 研究人员已经开发出许多方法来解决这些问题,包括忘记条目的方法,以便将数据库的大小保持在限定范围内。 本章末尾的书目和历史评论部分指出了一些相关文献,包括一些描述基于内存的学习应用于强化学习的论文。
9.10 基于核的函数近似¶
基于内存的方法,例如上述加权平均和局部加权回归方法,取决于在数据库中为示例 \(s^{\prime} \mapsto g\) 分配权重, 取决于 \(s^{\prime}\) 和查询状态 \(s\) 之间的距离。分配这些权重的函数称为 核函数,或简称为 核。 在加权平均和局部加权回归方法中,例如, 核函数 \(k : \mathbb{R} \rightarrow \mathbb{R}\) 为状态之间的距离分配权重。 更一般地说,权重不必取决于距离;它们可以依赖于状态之间的一些其他相似性度量。 在这种情况下,\(k : \mathcal{S} \times \mathcal{S} \rightarrow \mathbb{R}\), 因此 \(k(s, s^{\prime})\) 是关于 \(s^{\prime}\) 的数据的权重, 其对回答关于 \(s\) 的查询的影响。
从略微不同的角度来看,\(k(s, s^{\prime})\) 是从 \(s^{\prime}\) 到 \(s\) 的泛化强度的度量。 核函数以数字方式表达任何状态对任何其他状态的 相关 知识。 作为示例,图9.11中所示的铺片编码的泛化的强度对应于由均匀和非对称铺片偏移导致的不同核函数。 虽然铺片编码在其操作中没有明确地使用核函数,但是它根据一个进行了泛化。 实际上,正如我们在下面讨论的那样,线性参数函数近似导致的泛化强度总是可以用核函数来描述。
核回归 是基于内存的方法,它计算存储在内存中的 所有 示例的目标的核加权平均值,将结果分配给查询状态。 如果 \(\mathcal{D}\) 是存储示例的集合, 并且 \(g(s^{\prime})\) 表示存储示例中状态 \(s^{\prime}\) 的目标, 则核回归近似目标函数,在这种情况下是取决于 \(\mathcal{D}\) 的价值函数,即
上述加权平均方法是一种特殊情况,其中 \(k(s, s^{\prime})\) 仅在 \(s\) 和 \(s^{\prime}\) 彼此接近时才为非零,因此不需要在所有 \(\mathcal{D}\) 上计算总和。
常见的核是在第9.5.5节中描述的RBF函数近似中使用的高斯径向基函数(RBF)。 在那里描述的方法中,RBF是其中心和宽度从一开始就是固定的特征,其中心可能集中在预期许多示例落下的区域中,或者在学习期间以某种方式调整。 除非调整中心和宽度的方法,这是一种线性参数方法,其参数是每个RBF的权重,通常通过随机梯度或半梯度下降来学习。 近似的形式是预定RBF的线性组合。使用RBF核的核回归在两个方面与此不同。 首先,它是基于内存的:RBF以存储的示例的状态为中心。其次,它是非参数的:没有要学习的参数;对查询的响应由(9.23)给出。
当然,对于核回归的实际实现,必须解决许多问题,这些问题超出了我们简短讨论的范围。 然而,事实证明,任何线性参数回归方法,如我们在9.4节中描述的那样, 状态由特征向量 \(\mathbf{x}(s)=(x_{1}(s), x_{2}(s), \ldots, x_{d}(s))^{\top}\) 表示, 可以重铸为核回归,其中 \(k(s, s^{\prime})\) 是 \(s\) 和 \(s^{\prime}\) 的 特征向量表示的内积;即
使用此核函数的核回归产生与线性参数方法相同的近似值,如果它使用这些特征向量并使用相同的训练数据进行学习。
我们跳过了数学上的理由,这可以在任何现代机器学习文本中找到,例如Bishop(2006),并简单地指出一个重要的含义。 与其为线性参数函数近似器构造特征,我们可以直接构造核函数而不必完全引用特征向量。 并非所有核函数都可以表示为(9.24)中的特征向量的内积,但是可以表示为这样的核函数可以提供优于等效参数方法的显着优势。 对于许多特征向量集,(9.24)具有紧凑的函数形式,无需在 \(d\) 维特征空间中进行任何计算即可对其进行求值。 在这些情况下,核回归远不如使用带有特征向量表示的状态的线性参数方法复杂。 这就是所谓的“核技巧”,它允许在广阔的特征空间的高维度上有效地工作,同时实际上只使用存储的训练示例集。 核技巧是许多机器学习方法的基础,研究人员已经展示了它有时如何有利于强化学习。
9.11 深入研究在策略学习:兴趣和重点¶
我们在本章中到目前为止所考虑的算法已经同等地处理了所有遇到的状态,就像它们都同样重要。 但是,在某些情况下,我们对某些状态比其他状态更感兴趣。 例如,在折扣的回合问题中,我们可能更有兴趣准确评估回合中的早期状态,而不是后期状态, 在这些状态下,折扣可能使得奖励对起始状态的价值不那么重要。 或者,如果正在学习动作价值函数,那么准确评估价值远低于贪婪行为的不良行为可能就不那么重要了。 函数近似资源总是有限的,如果它们以更有针对性的方式使用,那么性能可以得到改善。
我们同等对待遇到的所有状态的一个原因是,我们正在根据在策略分布进行更新,对此,半梯度方法可获得更强的理论结果。 回想一下,在策略分布被定义为在遵循目标策略的同时在MDP中遇到的状态分布。现在我们将大大泛化这一概念。 我们将拥有许多在策略分布,而不是为MDP提供一个在策略分布。 所有这些都将具有共同点,即它们是在遵循目标策略的同时在轨迹中遇到的状态分布,但它们在某种意义上的轨迹如何开始会有所不同。
我们现在介绍一些新概念。首先,我们引入一个非负标量度量,一个称为 兴趣 的随机变量 \(I_t\), 表示我们对在时间 \(t\) 准确评估状态(或状态-动作对)感兴趣的程度。 如果我们根本不关心状态,那么兴趣应该是零;如果我们完全关心,它可能是一,虽然它被正式允许采取任何非负值。 兴趣可以以任何因果关系设定;例如,它可以取决于直到时间 \(t\) 的轨迹或在时间 \(t\) 的学习参数。 然后将 \(\overline{\mathrm{VE}}\) (9.1)中的分布 \(\mu\) 定义为 在遵循目标策略时遇到的状态分布,由兴趣加权。 其次,我们引入另一个非负标量随机变量,称为 重点 \(M_t\)。 该标量乘以学习更新,从而强调或不强调在时间 \(t\) 完成的学习。替换(9.15)的一般n步学习规则是
由(9.16)给出的n步回报,并且通过以下方式从兴趣中递归确定重点:
其中对于所有 \(t<0\),\(M_t\doteq 0\)。这些等式被认为包括蒙特卡罗情况, 其中 \(G_{t:t+n}=G_{t}\),所有更新都在回合结束时进行,\(n=T-t\),并且 \(M_{t}=I_{t}\)。
例9.4说明了兴趣和重点如何能够产生更准确的价值估计。
例9.4 兴趣和重点
要了解使用兴趣和重点的潜在好处,请考虑以下所示的四状态马尔可夫奖励流程:
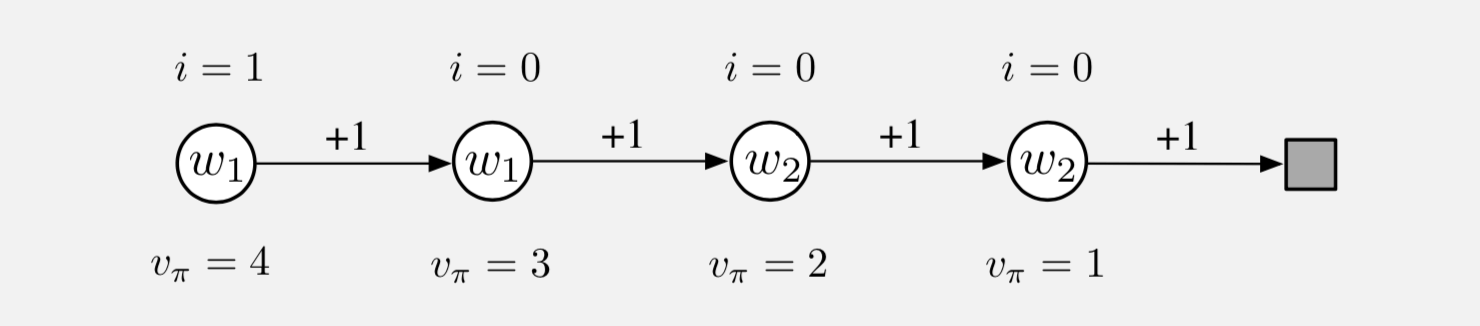
回合从最左边的状态开始,然后在每一步上向右转换一个状态,奖励为+1,直到达到终点状态。 因此,第一状态的真实值是4,第二状态真实值是3,依此类推,如每个状态下所示。 这些都是真正的价值;估计值只能接近这些值,因为它们受参数化的约束。 参数矢量 \(\mathbf{w}=\left(w_{1}, w_{2}\right)^{\top}\) 有两个分量,参数化是在每个状态内写入的。 前两个状态的估计值仅由 \(w_1\) 给出,因此即使它们的真值不同,也必须相同。 类似地,第三和第四状态的估计值仅由 \(w_2\) 给出,即使它们的真实值不同,也必须相同。 假设我们有兴趣仅准确评估最左边的状态;如上所述,我们为其分配1的兴趣,而所有其他状态的兴趣为0。
首先考虑应用梯度蒙特卡罗算法来解决这个问题。 本章前面介绍的算法没有考虑到兴趣和重点(在(9.7)和(9.3)的方框中) 会收敛(用于减小步长)到参数向量 \(\mathbf{w}_{\infty}=(3.5,1.5)\), 这给出了第一个状态_我们唯一感兴趣的一个,值为3.5(即介于第一和第二状态的真值之间)。 另一方面,本节中提出的使用兴趣和重点的方法将正确地学习第一个状态的价值; \(w_1\) 将收敛到4,而 \(w_2\) 永远不会更新,因为除了最左边的所有状态,重点为零。
现在考虑应用两步半梯度TD方法。 本章前面没有兴趣和重点的方法(在(9.15)和(9.16)以及(9.4)的方框中) 将再次收敛到 \(\mathbf{w}_{\infty}=(3.5,1.5)\), 而有兴趣和重点的方法收敛到 \(\mathbf{w}_{\infty}=(4,2)\)。 后者为第一个状态和第三个状态(第一个状态自举来源)产生完全正确的值,并不对应于第二或第四状态进行任何更新。
9.12 总结¶
如果强化学习系统要适用于人工智能或大型工程应用,则必须能够进行 泛化。 为了实现这一点,可以简单地通过将每个更新视为训练样例,使用用于 监督学习函数近似 的任何广泛的现有方法。
也许最合适的监督学习方法是使用 参数化函数近似 的方法,其中策略由权向量 \(\mathbf{w}\) 参数化。 虽然权重向量有很多分量,但状态空间仍然大得多,我们必须找到一个近似的解决方案。 我们将 均方值误差 \(\overline{VE}(\mathbf{w})\) 定义为 在策略分布 \(\mu\) 下 权重向量 \(\mathbf{w}\) 的值 \(v_{\pi_{\mathbf{w}}}(s)\) 中的误差的度量。 \(\overline{VE}\) 为我们提供了一种明确的方法,可以在在策略案例中对不同的价值函数近似进行排序。
为了找到一个好的权重向量,最流行的方法是 随机梯度下降 (SGD)的变化。 在本章中,我们重点关注具有 固定策略 的 在策略 案例,也称为策略评估或预测; 这种情况下的自然学习算法是 n步半梯度TD,其包括梯度蒙特卡罗和半梯度TD(0)算法 作为 \(n=\infty\) 和 \(n=1\) 的特殊情况。半梯度TD方法不是真正的梯度方法。 在这种自举方法(包括DP)中,权重向量出现在更新目标中,但在计算梯度时不考虑这一点──因此它们是 半 梯度方法。 因此,他们不能依赖于经典的SGD结果。
然而,在 线性 函数近似的特殊情况下,半梯度方法可以获得良好的结果, 其中价值估计是特征的总和乘以相应的权重。线性情况在理论上是最容易理解的,并且在提供适当特征时在实践中工作良好。 选择特征是将先前领域知识添加到强化学习系统的最重要方法之一。 它们可以被选择为多项式,但是这种情况在通常在强化学习中考虑的在线学习设置中很难感化。 更好的是根据傅立叶基选择特征,或者根据稀疏重叠感受域的某种形式的粗编码。 铺片编码是粗编码的一种形式,其特别具有计算效率和灵活性。 径向基函数对于一维或二维任务非常有用,其中平滑变化的响应很重要。 LSTD是数据最有效的线性TD预测方法,但需要与权重数的平方成比例的计算,而所有其他方法在权重数量上具有线性复杂性。 非线性方法包括通过反向传播训练的人工神经网络和SGD的变化;这些方法近年来以 深度强化学习 的名义变得非常流行。
对于所有 \(n\),线性半梯度n步TD保证在标准条件下 收敛到最佳误差范围内的 \(\overline{VE}\) (通过蒙特卡罗方法渐近实现)。 对于更高的n,这个界限总是更紧,并且对于 \(n \rightarrow \infty\) 来说接近零。 然而,在实践中,非常高的n导致学习非常缓慢,并且一定程度的自举(\(n<\infty\))通常是可取的, 正如我们在第7章中的表格n步法和和第5章中表格TD和蒙特卡罗方法的比较中所看到的那样。
书目和历史评论¶
泛化和函数逼近似一直是强化学习的一个组成部分。Bertsekas和Tsitsiklis(1996),Bertsekas(2012) 和Sugiyama等(2013)介绍了强化学习中函数近似的最新技术。本节末尾讨论了强化学习中函数近似的一些早期工作。
9.3 用于最小化监督学习中的均方误差的梯度下降方法是众所周知的。 Widrow和Hoff(1960)引入了最小均方(LMS)算法,该算法是原型增量梯度下降算法。许多文本中提供了该算法和相关算法的细节 (例如,Widrow和Stearns,1985;Bishop,1995;Duda和Hart,1973)。
Sutton(1984,1988)首先探讨了半梯度TD(0),作为我们将在第12章中讨论的线性TD(\(\lambda\))算法的一部分。 描述这些自举方法的术语“半梯度”是新出现在本书的第二版。
在强化学习中最早使用状态聚合可能是Michie和Chambers的BOXES系统(1968)。 强化学习中的状态聚合理论由Singh,Jaakkola和Jordan(1995)以及Tsitsiklis和Van Roy(1996)开发。 状态聚合从一开始就被用于动态规划(例如,Bellman,1957a)。
9.4 Sutton(1988)证明了对于特征向量 \(\{\mathbf{x}(s) : s \in \delta\}\) 线性无关的情况, 平均线性TD(0)与最小 \(\overline{\mathrm{VE}}\) 解的收敛性。 几个研究人员几乎同时证明了概率为1的收敛性(Peng,1993;Dayan和Sejnowski,1994;Tsitsiklis,1994;Gurvits,Lin和Hanson,1994)。 此外,Jaakkola,Jordan和Singh(1994)证明了在线更新下的融合。 所有这些结果都假设线性独立的特征向量,这意味着至少与 \(\mathbf{w}_t\) 有状态一样多的分量。 Dayan(1992)首先展示了一般(依赖)特征向量的更重要情况的收敛性。 Tsitsiklis和Van Roy(1997)证明了Dayan结果的重大泛化和强化。 他们证明了本节提出的主要结果,即线性自举方法的渐近误差的界限。
9.5 我们对线性函数近似的可能性范围的介绍是基于Barto(1990)的。
9.5.2 Konidaris,Osentoski和Thomas(2011)以简单的形式介绍了傅里叶基, 该形式适用于具有多维连续状态空间和不必是周期函数的强化学习问题。
9.5.3 粗编码 一词是由Hinton(1984)提出的,而我们的图9.6是基于他的一个数字。 Waltz和Fu(1965)在强化学习系统中提供了这种函数近似的早期例子。
9.5.4 Albus(1971,1981)介绍了铺片编码,包括散列。 他用他的“小脑模型咬合架控制器”或CMAC来描述它,因为铺片编码有时在文献中已知。 术语“铺片编码”是本书第一版的新内容,尽管用这些术语描述CMAC的想法来自Watkins(1989)。 铺片编码已被用于许多强化学习系统(例如,Shewchuk和Dean,1990;Lin和Kim,1991; Miller,Scalera和Kim,1994;Sofge和White,1992;Tham,1994;Sutton,1996;Watkins,1989) 以及其他类型的学习控制系统(例如,Kraft和Campagna,1990; Kraft,Miller和Dietz,1992)。 本节重点介绍了Miller和Glanz(1996)的工作。用于铺片编码的通用软件有多种语言版本 (例如,参见http://incompleteideas.net/tiles/tiles3.html)。
9.5.5 使用径向基函数的函数近似自Broomhead和Lowe(1988)与人工神经网络相关以来一直受到广泛关注。 Powell(1987)回顾了RBF的早期用途,并且Poggio和Girosi(1989,1990)广泛开发并应用了这种方法。
9.6 自适应步长参数的方法包括RMSprop(Tiele-man和Hinton,2012),Adam(Kingma和Ba,2015), 随机元下降方法,如Delta-Bar-Delta(Jacobs,1988),其增量泛化(Sutton,1992b,c; Mahmood等,2012), 以及非线性泛化(Schraudolph,1999,2002)。明确设计用于强化学习的方法包括AlphaBound(Dabney和Barto,2012), SID和NOSID(Dabney,2014),TIDBD(Kearney等,准备中)以及 随机元下降在策略梯度学习中的应用( Schraudolph,Yu和Aberdeen,2006)。
9.6 由McCulloch和Pitts(1943)引入阈值逻辑单元作为抽象模型神经元是人工神经网络的开始。 作为分类或回归学习方法的人工神经网络的历史经历了几个阶段: 粗略地,Perceptron(Rosenblatt,1962)和ADALINE(ADAptive LINear Element) (Widrow和Hoff,1960)的单层人工神经网络学习阶段, 多层人工智能学习的误差反向传播阶段(LeCun,1985; Rumelhart,Hinton和Williams,1986), 以及当前深度学习阶段,强调表征学习 (例如,Bengio,Courville和Vincent, 2012; Goodfellow,Bengio和Courville,2016)。 关于人工神经网络的许多书籍的例子是Haykin(1994),Bishop(1995)和Ripley(2007)。
人工神经网络作为强化学习的函数近似可以追溯到Farley和Clark(1954)的早期工作, 他使用类似强化的学习来修改代表策略的线性阈值函数的权重。 Widrow,Gupta和Maitra(1973)提出了一种类似神经元的线性阈值单元,它实现了一种学习过程, 他们称之为 学习与批评或选择性自举适应,ADALINE算法的强化学习变体。 Werbos(1987,1994)开发了一种预测和控制方法,该方法使用通过误差反向训练训练的ANN来使用类似TD的算法来学习策略和价值函数。 Barto,Sutton和Brouwer(1981)以及Barto和Sutton(1981b)将联想记忆网络 (例如,Kohonen,1977; Anderson,Silverstein,Ritz和Jones,1977)的观点扩展到强化学习。 Barto,Anderson和Sutton(1982)使用双层ANN来学习非线性控制策略,并强调了第一层学习合适表示的作用。 Hampson(1983,1989)是学习价值函数的多层人工神经网络的早期支持者。 Barto,Sutton和Anderson(1983)以人工神经网络学习的形式提出了一种演员评论算法来平衡模拟极点(见第15.7和15.8节)。 Barto和Anandan(1985)引入了随机版Widrow等人(1973)的选择性自举算法, 称为 关联奖励惩罚 (\(A_{R-P}\)) 算法。Barto(1985,1986)和Barto和Jordan(1987) 描述了由 \(A_{R-P}\) 单元组成的多层ANN,该 \(A_{R-P}\) 单元用全局广播强化信号训练, 以学习不可线性分离的分类规则。Barto(1985)讨论了人工神经网络的这种方法,以及当时这类学习规则与文献中的其他规则有何关联。 (关于训练多层人工神经网络的这种方法的其他讨论,请参阅第15.10节。) Anderson(1986,1987,1989)评估了多种训练多层人工神经网络的方法, 并展示了演员和评论家都在其中实施的演员评论算法通过误差反向传播训练的双层人工神经网络在Hanoi任和杆平衡中优于单层人工神经网络。 Williams(1988)描述了几种可以将反向传播和强化学习结合起来用于训练人工神经网络的方法。 Gullapalli(1990)和Williams(1992)设计了具有连续而非二元输出的神经元样单元的强化学习算法。 Barto,Sutton和Watkins(1990)认为人工神经网络可以在近似求解顺序决策问题所需的函数方面发挥重要作用。 Williams(1992)将REINFORCE学习规则(第13.3节)与用于训练多层人工神经网络的误差反向传播方法联系起来。 Tesauro的TD-Gammon(Tesauro 1992,1994;第16.1节)有效地展示了TD(\(\lambda\))算法的学习能力, 其中多层ANN在学习玩十五子棋时具有函数逼近。 Silver等人的AlphaGo,AlphaGo Zero和AlphaZero程序(2016,2017a,b; 16.6节)使用深度卷积神经网络的强化学习, 在围棋游戏中取得了令人瞩目的成果。Schmidhuber(2015)回顾了人工神经网络在强化学习中的应用,包括递归人工神经网络的应用。
9.8 LSTD应归功于Bradtke和Barto(见Bradtke,1993,1994; Bradtke和Barto,1996;Bradtke,Ydstie和Barto,1994), 并由Boyan(1999,2002),Nedi c和Bertsekas(2003)和Yu(2010)进一步发展。 至少自1949年以来已知逆矩阵的增量更新(Sherman和Morrison,1949)。Lagoudakis和Parr(2003; Buşoniu,Lazaric,Ghavamzadeh,Munos,Babŭska和De Schutter,2012)介绍了最小二乘法控制的扩展。
9.9 我们对基于内存的函数近似的讨论主要基于Atkeson,Moore和Schaal(1997)对局部加权学习的回顾。 Atkeson(1992)讨论了在基于内存的机器人学习中使用局部加权回归,并提供了涵盖该思想历史的广泛参考书目。 Stanfill和Waltz(1986)对人工智能中基于内存的方法的重要性进行了有影响力的论证,特别是考虑到随后可用的并行架构,例如连接机器。 Baird和Klopf(1993)引入了一种新的基于内存的方法,并将其用作应用于杆平衡任务的Q-learning的函数近似方法。 Schaal和Atkeson(1994)将局部加权回归应用于机器人杂耍控制问题,用于学习系统模型。 Peng(1995)使用杆平衡任务来试验几种最近邻方法,用于近似价值函数,策略和环境模型。 Tadepalli和Ok(1996)通过局部加权线性回归获得了有希望的结果,以学习模拟自动引导车辆任务的价值函数。 Bottou和Vapnik(1992)在一些模式识别任务中证明了与非局部算法相比,几种局部学习算法的惊人效率,讨论了局部学习对泛化的影响。
Bentley(1975)引入了k-d树,并报告了在n个记录上观察最近邻搜索的 \(O(\log n)\) 的平均运行时间。 Friedman,Bentley和Finkel(1977)阐述了使用k-d树进行最近邻搜索的算法。 Omohundro(1987)讨论了使用k-d树等分层数据结构实现的效率提升。 Moore,Schneider和Deng(1997)介绍了使用k-d树进行有效的局部加权回归。
9.10 核回归的起源是Aizerman,Braverman和Rozonoer(1964)*潜在函数的方法*。 他们将数据比作指向空间分布的各种符号和数量的电荷。通过对点电荷的电位求和而产生的在空间上产生的电势对应于插值曲面。 在这个类比中,核函数是点电荷的势能,它作为距电荷距离的倒数而下降。 Connell和Utgoff(1987)将一个演员评论方法应用于杆平衡任务,其中评论家使用具有反距离加权的核回归来近似值函数。 由于对机器学习中核回归的广泛兴趣,这些作者没有使用术语核,而是提到了“Shepard的方法”(Shepard,1968)。 其他基于核的强化学习方法包括Ormoneit和Sen(2002),Dietterich和Wang(2002), Xu,Xie,Hu和Lu(2005),Taylor和Parr(2009),Barreto,Precup和Pineau (2011年), Bhat,Farias和Moallemi(2012年)。
9.11 对于Emphatic-TD方法,请参阅第11.8节的书目注释。
我们知道函数近似方法用于学习价值函数的最早的例子是Samuel的跳棋运动员(1959,1967)。 Samuel遵循Shannon(1950)的建议,即价值函数不必精确地成为选择游戏中移动的有用指南,并且它可能通过线性特征组合来近似。 除了线性函数近似之外,Samuel还尝试使用称为签名表的查找表和分层查找表 (Grith,1966,1974; Page,1977; Biermann,Fairfield,and Beres,1982)。
与Samuel的工作大致相同,Bellman和Dreyfus(1959)提出使用函数近似方法和DP。 (很有可能认为Bellman和Samuel彼此之间有一些影响,但我们知道在两者的工作中都没有提到另一个。) 现在有关于函数近似方法和DP的相当广泛的文献,例如多重网格方法,以及使用样条和正交多项式的方法。 (例如,Bellman和Dreyfus,1959;Bellman,Kalaba和Kotkin,1973;Daniel,1976; Whitt,1978;Reetz,1977; Schweitzer和Seidmann,1985;Chow和Tsitsiklis,1991; Kushner和Dupuis,1992;Rust,1996)。
Holland(1986)分类器系统使用选择性特征匹配技术来泛化跨状态-动作对的评估信息。 每个分类器匹配具有特征子集的指定值的状态子集,其余特征具有任意值(“通配符”)。 然后将这些子集用于传统的状态聚合方法中以进行函数近似。 Holland的想法是使用遗传算法来发展一组分类器,这些分类器共同实现一个有用的动作-价值函数。 荷兰的思想影响了作者对强化学习的早期研究,但我们关注的是函数逼近的不同方法。 作为函数近似器,分类器在几个方面受到限制。首先,它们是状态聚合方法,在缩放和高效表示平滑函数方面具有相应的限制。 此外,分类器的匹配规则只能实现与特征轴平行的聚合边界。 也许传统分类器系统最重要的限制是分类器是通过遗传算法学习的,这是一种进化方法。 正如我们在第1章中讨论的那样,在学习过程中可以获得有关如何学习的更多详细信息,而不是进化方法可以使用的信息。 这种观点使我们改为采用监督学习方法来强化学习,特别是梯度下降和人工神经网络方法。 Holland的方法和我们的方法之间的这些差异并不令人惊讶,因为Holland的思想是在人工神经网络被普遍认为计算能力太弱而无用的时期发展起来的, 而我们的工作是在这个时期开始时广泛质疑一般常识。结合这些不同方法的各个方面仍有很多机会。
Christensen和Korf(1986)用国际象棋游戏中的线性值函数近似修正系数的回归方法进行了实验。 Chapman和Kaelbling(1991)和Tan(1991)采用决策树方法来学习价值函数。 基于解释的学习方法也适用于学习价值函数,产生紧凑的表示 (Yee,Saxena,Utgoff和Barto,1990;Dietterich和Flann,1995)。
| [1] | \(^{\top}\) 表示转置,此处需要将文本中的水平行向量转换为垂直列向量; 在本书中,除非明确地水平写入或转置,否则向量通常被认为是列向量。 |
| [2] | 有些多项式族比我们讨论的更复杂,例如,正交多项式的不同族,这些可能更好, 但目前在强化学习中几乎没有经验。 |